【基本】正負の数の加法
ここでは、正の数や負の数の加法(足し算)について見ていきます。
正の数同士の足し算を数直線上で考えてみよう
小学校では、数を学んだ後には、足したり引いたりといった計算の方法を学びました。中学でも、負の数を学んだ後は、負の数の計算方法について学んでいきます。
まずは、足し算について見ていきます。なお、足し算のことを加法(かほう、addition)や加算ということもあります。また、足し算の結果を、和(sum) ともいいます。
正の数同士の足し算は簡単ですね。 $(+2)+(+3)$ というのは、 $2+3$ と同じことなので、小学校で見たときと同じように計算します。 $5$ が答えです。
問題は、負の数同士や、正の数と負の数が混じっている場合です。 $(-2)+(-3)$ とか $(+2)+(-3)$ などはどのように計算すればいいでしょう。
これを考えるためには、【導入】気温と負の数の引き算で見たように、気温を使って考えることもできますが、ここでは、数学でよく使われる数直線に関連させて考えることにしましょう。
数直線上で、 $(+2)+(+3)$ の答えである $5$ と $+2,+3$ とを見比べてみると、次のように対応していることがわかるでしょう。
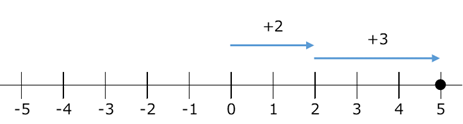
$+2$ とは、基準である $0$ より $2$ だけ大きな数で、 $+3$ は基準である $0$ より $3$ だけ大きな数なので、2つを合わせると、 $0$ よりも $5$ 大きな数になります。これを数直線で考えれば、 $+2$ の点から、さらに $3$ だけ右に移動したところが、 $(+2)+(+3)$ に対応する、と考えることができます。
このように、数直線上の移動に対応させて考えると、負の数に関する足し算も計算することができます。
負の数同士の足し算
先ほどの数直線上の移動に関連させて、負の数同士の計算を考えてみましょう。
$(-2)+(-3)$ を考えてみましょう。 $-3$ とは、基準よりも $3$ だけ小さい数を表すので、数直線では、 $-2$ から左に $3$ だけ移動したところに対応すると考えることができます。
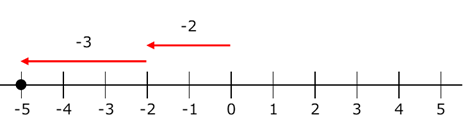
移動距離を合計( $2+3=5$ )し、マイナスをつければいいことがわかります。もう少し正確にいうと、絶対値同士を足して、マイナスをつけるということです(参考:【基本】絶対値と数と大小)。
これを踏まえて、別の計算もしてみましょう。
(1) $(-3)+(-5)$
(2) $(-1.2)+(-2.3)$
負の数同士の足し算は、数直線で考えると、絶対値同士を足した分だけ左に移動することに対応します。なので、絶対値同士を足して、マイナスをつければ答えになります。
(1)は、絶対値は、それぞれ、 $3,5$ となるので、和は $8$ です。これにマイナスをつけて、 $-8$ となります。
(2)は、絶対値は、それぞれ、 $1.2$ と $2.3$ となるので、和は $3.5$ です。これにマイナスをつけて、 $-3.5$ となります。このように計算できます。
正の数と負の数の足し算
数直線上での移動に関連させて、正の数と負の数の足し算も考えてみましょう。
正の数を足すことが右への移動、負の数を足すことが左への移動に対応していることがわかっていれば、他の計算も同じように計算できます。
$(+2)+(-3)$ について考えてみましょう。これは、数直線上で、原点から右へ $2$ 移動したところから、さらに左へ $3$ 移動する、ということに対応します。
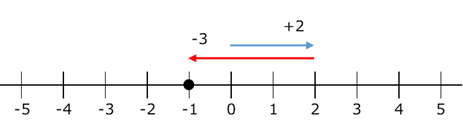
この図から、答えは $-1$ であることがわかります。
正の数と負の数を足す場合は、移動する方向が逆になります。先ほどの例であれば、右に $2$ 、左に $3$ 移動するので、最終的に、左に $3-2$ だけ移動することになります。移動する距離は、引き算で求めることになります。「足し算」といっているのに、「引き算」をするんですね。最後に、絶対値が大きい方の符号をつけておしまいです。
練習してみましょう。
(1) $(+13)+(-9)$
(2) $(-11)+(+3)$
(1)を考えます。数直線上で考えると、右へ $13$ 、左へ $9$ 移動するということなので、最終的には、原点から $13-9=4$ だけ離れた点に移動することがわかります。移動する方向は右ですね。なので、\[ (+13)+(-9)=4 \]となります。
(2)は、負の数と正の数を足す問題ですが、考え方は同じです。数直線上で考えると、左へ $11$ 、右へ $3$ 移動するということなので、最終的には、原点から $11-3=8$ だけ離れた点に移動することがわかります。移動する方向は左です。なので、\[ (-11)+(+3)=-8 \]となります。
慣れるまでは、数直線上での移動で考えるといいでしょう。
おわりに
ここでは、正の数と負の数の加法について見てきました。最後に、言葉で計算の仕方をまとめておきましょう。
異符号の和は、絶対値の大きい方から小さい方を引き、絶対値が大きい方の符号をつけた数。
言葉で書くと難しいですが、内容は上で見たのと同じ内容です。数直線で考えてみましょう。同符号の場合は、同じ方向に移動するので、移動する距離は足せばいいんですね。移動する方向は、もとの数と同じなので、共通の符号をつける、ということです。
異符号の場合は、移動する方向が逆です。移動は打ち消し合うため、最終的な移動距離は引いて求めることになります。移動する方向は、絶対値が大きい方となります。