【基本】正負の数の加法の性質
ここでは、正の数や負の数の加法(足し算)の性質について見ていきます。
正の数や負の数の加法の復習
正の数や負の数の加法(足し算)は、【基本】正負の数の加法で見ましたが、もう一度整理しておきましょう。
まず、正の数同士の和を、数直線で考えてみました。数直線上で、 $(+2)+(+3)=5$ は、次のように考えることができます。
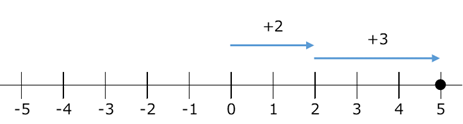
$+2$ が右へ $2$ 移動すること、 $+3$ が右へ $3$ 移動することに対応します。なので、和は、原点 $0$ から右へ $5$ 移動した点に対応する、ということですね。
これを踏まえて、負の数同士の和は、左への移動を使って、同じように考えればいいのでした。数直線上で $(-2)+(-3)$ は、次のように考えます。
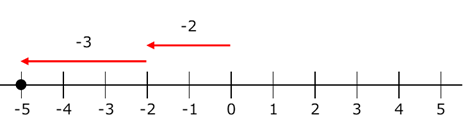
左へ $2$ 移動し、さらに左へ $3$ 移動するので、合計で左へ $5$ だけ移動することになります。なので、\[ (-2)+(-3)=-5 \]と計算します。正の数同士の和や負の数同士の和は、絶対値を足して、共通の符号をつけて計算する、ということもできます。
最後に、正の数と負の数の和です。これも、数直線での移動で考えます。 $(+2)+(-3)$ は、次のように考えます。
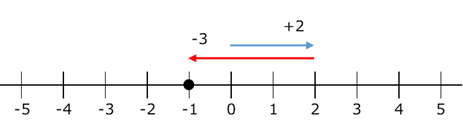
右へ $2$ 移動し、次に左へ $3$ 移動するので、合計で左へ $3-2=1$ だけ移動することになります。なので、\[ (+2)+(-3)=-1 \]と計算できます。符号が違う場合は、絶対値の大きい方から小さい方を引いて、絶対値が大きい方の符号をつけて計算する、ということです。
これらが、正の数や負の数の加法です。以下では、加法についての性質をいくつか見ていきます。
正の数や負の数の加法と0
数というのは、正の数と負の数以外に、 $0$ もあります(参考:【基本】符号のついた数)。 $0$ を足した場合はどうなるでしょうか。
答えを書くと、 $0$ を足しても、結果は変わりません。何も変化しないからですね。
$$\begin{aligned}
(-3)+0 &= -3 \\
0+(-4) &= -4
\end{aligned}$$という結果になります。
先ほど、正の数と負の数を足すときには、「絶対値の大きい方から小さい方を引いて、絶対値が大きい方の符号をつけて計算する」と書きましたが、絶対値が同じ場合はどうなるでしょうか。例えば、次のような場合です。\[ (-5)+(+5) \]符号が違っていて、絶対値はともに $5$ ですね。これを数直線上で考えてみましょう。すると、左へ $5$ 移動し、右へ $5$ 移動することに対応するので、原点に戻ってきますね。つまり、 $0$ です。符号が異なり、絶対値が同じ場合は、和は $0$ になります。\[ (-5)+(+5)=0 \]となります。
加法の交換法則
数直線の原点から出発して、「右へ $2$ 移動してから左へ $5$ 移動する」のと、「左へ $5$ 移動してから右へ $2$ 移動する」のとで、結果はどう変わるでしょうか。どちらの移動を先に行うかだけの違いなので、結果は同じですね。どちらでも、「原点から左へ $3$ 移動した点」にうつります。
これを和で考えれば、\[ (+2)+(-5)=(-5)+(+2) \]が成り立つということです。数を入れ替えて足しても、結果は変わりません。このことを、加法の交換法則(commutative law of addition) といいます。
例えば、 $(+5)+(-8)$ を計算するよりも、 $(-8)+(+5)$ のほうが計算しやすい、ということであれば、後者で計算してもいい、ということですね。
加法の結合法則
今後は、2つの数の和だけでなく、3つ以上の数の和を計算することも出てきます。基本的には前から計算していきますが、小学校では、足す順番を変えても答えは変わらないことを学びました。これは、負の数の場合にも成り立ちます。
例えば、\[ (-7)+(+3)+(+5) \]を計算するときに、「前の2つを足すと、符号が違うからイヤだなぁ。後ろの2つを先に足したいな」と考えて計算してもOKということです。\[ \{(-7)+(+3)\}+(+5) = (-7)+\{(+3)+(+5)\} \]ということですね。数直線上の移動で考えれば、どこから和を計算しても結果が変わらないことがわかるでしょう。この性質を、加法の結合法則(associative law of addition) といいます。
加法の交換法則や結合法則は、正の数のときに成り立つことは小学校で学びますが、負の数でも成り立つんですね。
(1) $(+29)+(-4)+(-29)$
(2) $(+1234)+(-4321)+(+8765)+(-5678)$
(1)は、前から順番に足すのは面倒そうですね。しかし、1つ目と3つ目の和を先に計算すると $0$ になります。足す順番を変えても答えは変わらないので、結局、答えは $-4$ だとわかります。
(2)は、前から計算していってももちろんいいのですが、符号が同じもので計算したほうが考えやすいかもしれません。1つ目と3つ目、2つ目と4つ目とペアを組んで計算すると
$$\begin{aligned}
& (+1234)+(-4321)+(+8765)+(-5678) \\[5pt]
=& (+1234)+(+8765)+(-4321)+(-5678) \\[5pt]
=& (+9999)+(-9999) \\[5pt]
=& 0 \\[5pt]
\end{aligned}$$となります。
おわりに
ここでは、正負の数の加法について、いくつかの性質を見てきました。交換法則や結合法則があるおかげで、足す順番を変えて計算することができます。楽に計算する方法がないか、考えて計算するようにしましょう。