【基本】円とおうぎ形
ここでは、円やおうぎ形に関する用語を見ていきます。【基本】点と直線などで見たように、すでに知っている内容も多いと思いますが、定義を確認しながら見ていきましょう。
円
ある点からの距離が一定である点の集まりを、円(circle) といいます。
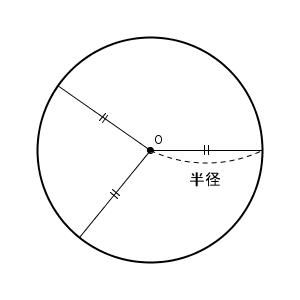
上の図で、点$\mathrm{O}$ のまわりにある点は、点$\mathrm{O}$ からの距離が一定となっています。この中央にある点を、円の中心(center) といい、中心からの距離のことを半径(はんけい、radius) といいます。中心が $\mathrm{O}$ の円を、円$\mathrm{O}$ と呼びます。
少しまぎらわしいのですが、「円」といった場合に、内側も含めることもあります。例えば、小学校のときにすでに「円の面積」を求めたことがあると思いますが、このときには円の内部も含めていることになります。こうしたことがあるので、内側を含めない部分をはっきりと表すために、まわりの曲線のことを円周(circumference) と呼びます。「円周」と言った場合、円の内側を入れることはありません。
また、これも紛らわしいのですが、円の中心と円周上の点とを結んだとき、この線分の長さを半径というのですが、この線分のことも半径ということがあります。つまり、「半径」というと、線分のことを言ってるかもしれないし、長さのことを言ってるかもしれない、ということです。
図形の世界では、こうしたことがよくあります。「円周」も、円のまわりの曲線を指すこともあるし、この曲線の長さを指すこともあります。どちらを指してるかは、文脈から読み取るしかありません。
円周の長さと円周率
半径を2倍したものを、直径(diameter) といいます。
円周の長さは、円の直径の比例します。円周の長さの、直径に対する比率を、円周率といいます。言い換えると、円周÷直径が円周率、ということです。これが円周率の定義です。この値は、円の大きさに関わらず一定で、 $3.141592\cdots$ と限りなく続いていく値です。この値のことを、 $\pi$ という文字で表します。
例えば、直径が $3$ cmの円の場合、円周の長さは $3\pi$ cmとなります。半径が $r$ cmの場合は、円周の長さは $2\pi r$ cmとなります。【基本】文字を使った式で表そう(円周率を使う場合)でも見たように、 $\pi$ を含んだ積で「×」を省略する場合、 $\pi$ は数字より後で他の文字よりも先に書きます。
小学校のときには、円周率を3.14として計算していましたが、中学の数学以降は、 $\pi$ を使うことがほとんどなので、小数の計算をする機会はすごく減ります。
弧と弦
円周上の2点$\mathrm{A, B}$ を結ぶことを考えてみましょう。
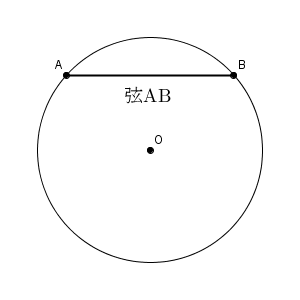
円周上の2点を結ぶ線分は、弦(げん、chord) といいます。ギターの弦と同じ字を使います。両端が $\mathrm{A, B}$の弦は、弦$\mathrm{AB}$ と書きます。
また、円周上の曲線のことを言いたいこともあります。これは、弧(こ、arc) といいます。両端が $\mathrm{A, B}$の弧は、弧$\mathrm{AB}$ と書きます。記号を使って $\stackrel{ \Large \frown }{ \mathrm{ AB } }$ とも書きます。

上の図を見てもわかりますが、弧$\mathrm{AB}$ は、2つあります。どちらかを特定したい場合は、「短い方」「長い方」と言って区別したりします。また、次のように弧の途中に別の点を含んでいることがあります。
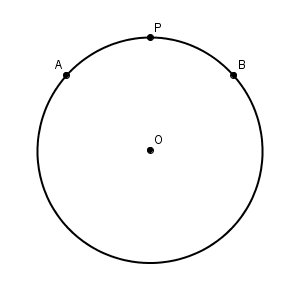
この場合、上の図のような場合に、短い方の弧のことを言いたいときは、 $\stackrel{ \Large \frown }{ \mathrm{ APB } }$ と書いたり、「弧$\mathrm{AB}$ の点$\mathrm{P}$ を含む方」と書いたりします。反対に、上の図のような場合に、長い方の弧のことを言いたいときは、「弧$\mathrm{AB}$ の点$\mathrm{P}$ を含まない方」と書いたりします。
おうぎ形
次の図のように、弧の両端をそれぞれ円の中心と結び、これらの線分と弧とで囲まれた図形をおうぎ形(circular sector) といいます。
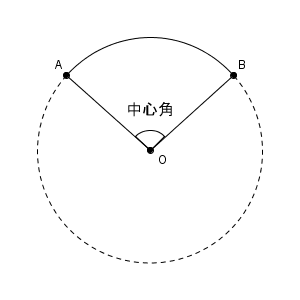
また、2つの半径で作られる角を、中心角といいます。円の中心にできる角だと考えれば覚えやすいですね。
ちなみに、おうぎは、漢字では「扇」と書きます。扇子(せんす)のことです。扇子を見たことがある人は、形が似ていることがわかるでしょう。
弧の長さ
おうぎ形にある曲線の部分も、弧といいます。この弧の長さは、次のように考えて求めます。

中心角が $60^{\circ}$ であれば、円を6つに分解したものの1つ分だと考えられます。別の言い方でいうと、円周の長さを $\dfrac{60}{360}=\dfrac{1}{6}$ 倍したもの、とも言えます。なので、上の図であれば、\[ 12\times 2\times \pi \times \frac{60}{360}=4\pi \]なので、 $4\pi$ cmだとわかります。
おうぎ形の弧の長さは、半径(または直径)と中心角がわかれば求めることができます。
なお、おうぎ形の周の長さと言われれば、弧の長さ以外に、2つの半径も含めないといけない点に注意しましょう。上の図でいえば、おうぎ形の周の長さは、 $(24+4\pi)$ cm となります。
おわりに
ここでは、円やおうぎ形に関連する用語を見てきました。また、円周の長さやおうぎ形の弧の長さを求める方法も見ました。円については、中学3年でもっと詳しく見ることになります。