【基本】点と直線との距離と作図
ここでは、点と直線との距離について見ていきます。また、垂線などの作図と距離との関係についても見ていきます。
点と直線との距離
2つの点 $\mathrm{A, B}$ があったとき、2点間の距離とは、線分 $\mathrm{AB}$ の長さのことを言います(参考:【基本】点と直線)。
これは、点 $\mathrm{A}$ から点 $\mathrm{B}$ に移動するときに、一番移動距離が短い場合を考えていることになります。
これを参考にすると、点と直線との距離はどう考えるのが自然でしょうか。
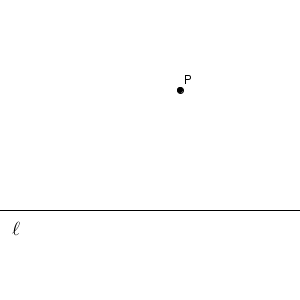
点 $\mathrm{P}$ から直線 $\ell$ へ移動するとき、一番移動距離が短くなるのはどのようなときでしょうか。点 $\mathrm{P}$ が自分の家で、 $\ell$ がまっすぐな川や道を想像してみてもいいでしょう。そうすると、最短で行くには、次のような経路がいいとわかると思います。

直線 $\ell$ に垂直で、点 $\mathrm{P}$ を通るような線に沿って移動するのが最短ですね。このときの移動距離を、点 $\mathrm{P}$ と直線 $\ell$ との距離といいます。厳密に書くと、次のようになります。
このような点 $\mathrm{Q}$ の作図のしかたは、【基本】垂線の作図(直線上にない点を通る)その2などで見ています。なので、点 $\mathrm{P}$ と直線 $\ell$ との距離と同じ長さの線分は作図できる、ということです。
直線と直線との距離
次のように、2つの平行な直線 $\ell,m$ があったとします。
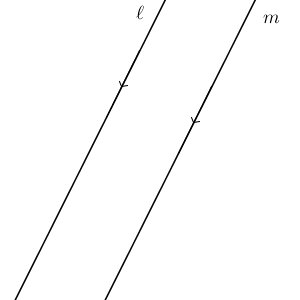
この2直線は、つねに同じだけ離れているように見えますね。もう少し正確にいうと、 $\ell$ 上のどの点をとっても、その点と直線 $m$ との距離は同じ、ということです。
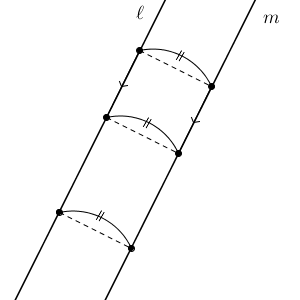
この一定の距離のことを、2直線 $\ell,m$ の距離といいます。
なお、2つの直線が平行でない場合は、どこかで交わってしまいます。そのため、この場合は、2直線の距離は考えません。
角の二等分線と距離
【基本】垂線二等分線の作図では、「線分 $\mathrm{AB}$ の垂直二等分線は、2点 $\mathrm{A, B}$ からの距離が等しい点の集まり」といえることを見ました。同じように、角の二等分線も、距離に関連する言葉で言い換えることもできます。
角の二等分線は、次のように作図するのでした。
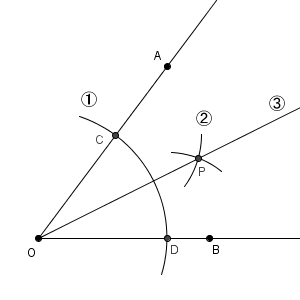
このようにしてできる角の二等分線の上に、1つ点をとり、それぞれの辺までの距離を考えてみましょう。

角の二等分線で折り返すと、図形はぴったりと重なることから、それぞれの辺までの距離はおなじであることがわかります。これは、角の二等分線上の他の点でも成り立ちます。

逆に、角の二等分線上にない点は、それぞれの辺までの距離は異なります。それは、【基本】垂線二等分線の作図のときと同じように示すことができます。
以上から、角の二等分線は、それぞれの辺からの距離が等しい点の集まりだということができます。
例題
最後に、距離に関する問題を見てみます。
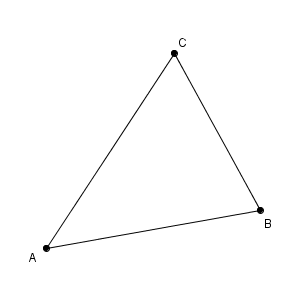
先ほど見たことから、2つの直線からの距離が等しい点の集まりが角の二等分線になるのでした。なので、辺 $\mathrm{AB, AC}$ からの距離が等しい点のあつまりは、 $\angle \mathrm{ A }$ の二等分線であることがわかります。
もし、この言いかえに気づかなかった場合は、完成図を考えてみましょう。どういうふうに作図するかは一旦置いておいて、点 $\mathrm{P}$ が作図できたとしたら、どのような図になるかを考えてみます。
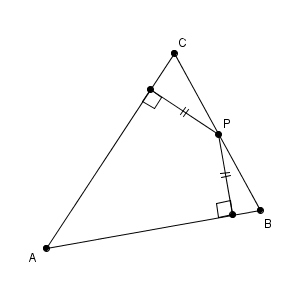
上の図の点 $\mathrm{P}$ は、辺 $\mathrm{AB, AC}$ からの距離が等しいことと、辺 $\mathrm{BC}$ 上にあることを満たしていますね。直線 $\mathrm{AP}$ で折れば、長さの等しい線分が重なることから、点 $\mathrm{P}$ は $\angle \mathrm{ A }$ の二等分線であることがわかります。
こうして、 $\angle \mathrm{ A }$ の二等分線と辺 $\mathrm{BC}$ との交点が、今の条件を満たすことがわかります。次のようにして、点 $\mathrm{P}$ が作図できます。
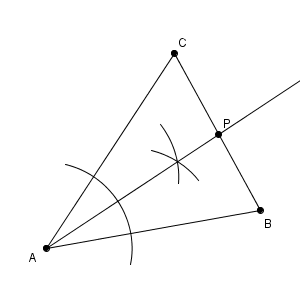
この問題のように、「角の二等分線を作図しなさい」とは書かれていませんが、角の二等分線を作図することもあります。
おわりに
ここでは、点と直線との距離、平行な2直線の距離について見てきました。また、角の二等分線を作図する問題を見ました。作図するものが直接的に(垂線や二等分線などと)指定されていない場合は、何を作図すればいいか考える必要があります。条件を満たすものがどういうものか、完成図から考える方法もあります。