【基本】垂線二等分線の作図
ここでは、垂直二等分線の作図方法について見ていきます。
中点と垂直二等分線
【基本】角の二等分線の作図では、角を二等分する直線を作図する方法を見ました。この二等分線には、もう一つ種類があります。線分を二等分する直線です。
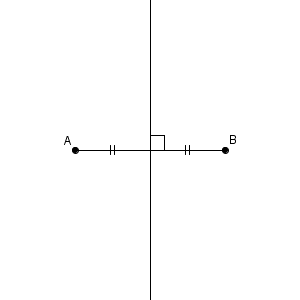
線分とは、【基本】点と直線でも見た通り、2点を通る直線のうち、2点とその間の部分をいいます。直線とは異なり、線分は両端の場所がわかっているので、ちょうど中間の点があります。このような、線分上の点のうち、線分の両端からの距離が等しい点のことを、中点(midpoint) といいます。
この中点を通り、この線分に垂直な直線を、垂直二等分線(line segment bisector) といいます。線分に垂直で、線分を二等分する線ということですね。
今まで、垂線の作図をしてきました。そのときに扱ったのは、「ある直線に垂直で、ある点を通る直線」でした。今回は、「中点を通る」ことはわかるものの、中点がどこかはわかりません。どのように作図すればいいでしょうか。以下で、見ていくことにしましょう。
垂直二等分線の作図
次のような線分 $\mathrm{AB}$ に対して、垂直二等分線を作図する方法を考えてみましょう。
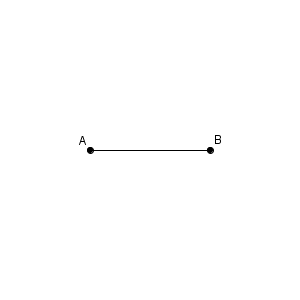
今まで、垂直な直線を作図するには、円を使って線対称な図形をかきました。今回も同じような手法で作図できないでしょうか。
円をかくには、中心と半径を決めないといけないですが、中心になりそうなところは、線分の両端しかないですね。それらを中心に円をかいてみましょう。
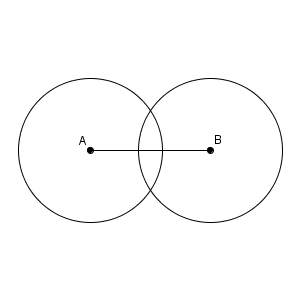
2つの円が交わるように書いてみました。この図は、【基本】垂線の作図(直線上にない点を通る)その1の作図方法と似ていますね。
違うところは、今回は、同じ半径を使って円をかいているところです。こうすると、図は、横の線に対しても、縦の線に対しても、線対称になることがわかります。

これは、【基本】2つの円と線対称な図形#2つの円と線対称その3でも見た内容ですね。
このことから、2つの交点を結ぶと、線分 $\mathrm{AB}$ を二等分し、線分 $\mathrm{AB}$ に垂直な線をひくことができます。

実際には、2つの円の交点がわかればいいので、上のように、円の一部をかくだけでかまいません。
線分の両端を中心とする円をかくことで、線分について線対称な図形ができます。また、2つの円の半径を同じにすることで、2円の交点を結んだ直線について線対称な図形ができます。最終的にできる直線は、前者から垂直であることがわかり、後者から線分の中点を通ることがわかります。こうして、この方法で、垂直二等分線が作図できることがわかります。
作図の流れをもう一度まとめておきましょう。「線分 $\mathrm{AB}$ の垂直二等分線」のかき方は、次のようになります。
- STEP.1線分の両端を中心とする円をかく2つの交点ができるように、点 $\mathrm{A, B}$ を中心とした同じ半径の円をかく
- STEP.2直線で結ぶ2つの交点を直線で結ぶ
同じ半径を使う点に注意しましょう。
2点からの距離が等しい点の作図
先ほどは、線分 $\mathrm{AB}$ の垂直二等分線を作図する方法を見ました。垂直二等分線とは、線分の中点を通り、線分に垂直な直線のことですが、中点がどこかがわからなくても垂直二等分線が作図できました。というよりも、垂直二等分線を作図することで、中点も作図できることがわかります。

上の図の点 $\mathrm{M}$ は、線分 $\mathrm{AB}$ とこの垂直二等分線との交点です。このとき、 $\mathrm{ AM=BM }$ となります。垂直二等分線は線対称の軸であり、垂直二等分線で折ると、線分 $\mathrm{AM, BM}$ が重なるからですね。
これは、線分 $\mathrm{AB}$ との交点に限らず、垂直二等分線上の点ならいつも成り立ちます。次のように、垂直二等分線上に点 $\mathrm{P}$ をとってみます。
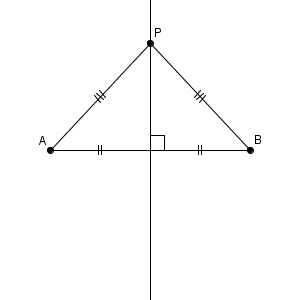
垂直二等分線で折ると、線分 $\mathrm{AP, BP}$ が重なるので、 $\mathrm{ AP=BP }$ が成り立ちます。
逆に、垂直二等分線にない点は、2点 $\mathrm{A, B}$ からの距離が等しくなることはありません。
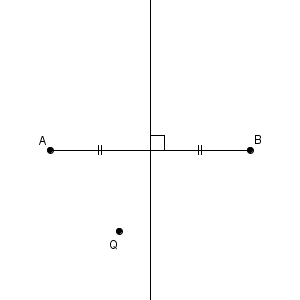
点 $\mathrm{Q}$ が線分 $\mathrm{AB}$ の垂直二等分線上になく、点 $\mathrm{A}$ 側にあるとしましょう。このとき、垂直二等分線について、点 $\mathrm{Q}$ と対称な点を点 $\mathrm{R}$ とし、線分 $\mathrm{QR}$ と垂直二等分線との交点を $\mathrm{S}$ とします。

このとき、 $\mathrm{ AQ=BR }$ となります。なので、もし、 $\mathrm{ AQ=BQ }$ とすると、 $\mathrm{ BQ=BR }$ となり、三角形 $\mathrm{BQR}$ は、二等辺三角形になってしまいます。すると、 $\mathrm{BS}$ で折り返すとぴったり重なるため、 $\mathrm{QR}$ と $\mathrm{BS}$ は垂直に交わるはずで、点 $\mathrm{B}$ が線分 $\mathrm{AB}$ の垂直二等分線上にあることになってしまいますが、そんなことは起こりません。なので、 $\mathrm{ AQ\ne BQ }$ となります。
点 $\mathrm{Q}$ が点 $\mathrm{B}$ 側にあるときも同様です。
つまり、線分 $\mathrm{AB}$ の垂直二等分線と、2点 $\mathrm{A, B}$ からの距離が等しい点の集まりは一致する、ということです。
このことを利用して、次のような例題を考えてみましょう。
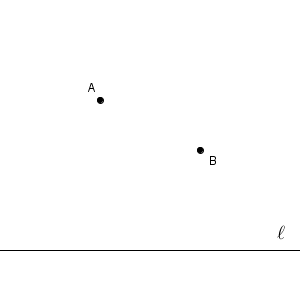
2点からの距離が等しい点を集めたものは、垂直二等分線と一致します。なので、線分 $\mathrm{AB}$ の垂直二等分線をひいて、それと直線 $\ell$ との交点を作図すれば、「直線 $\ell$ 上の点で、2点 $\mathrm{A, B}$ からの距離が等しい点」が作図できます。

このように、「垂直二等分線を作図しなさい」と言われていなくても、垂直二等分線を作図することがあります。
おわりに
ここでは、垂直二等分線の作図方法を見てきました。また、垂直二等分線が、線分の両端からの距離が等しい点の集まりであることも見ました。「垂直二等分線を作図しなさい」と直接言われないような出題のされ方もあるので、垂直二等分線の特徴も理解しておきましょう。