【基本】垂線の作図（直線上にない点を通る）その１

ここでは、ある点からある直線へ垂線をひく方法を見ていきます。

2つの円と線対称な図形の復習

このページでは、ある点を通り、ある直線に垂直な直線をひく方法を見ていきます。そのために、【基本】2つの円と線対称な図形で見た、次の図を参考にします。

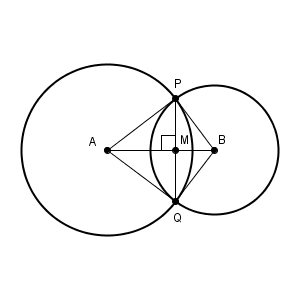
直線 $\mathrm{AB}$ で折り返せば、 $\angle \mathrm{ AMP }$ と $\angle \mathrm{ AMQ }$ がぴったり重なることから、どちらも90度であることがわかります。なので、 $\mathrm{ AB }\perp\mathrm{ PQ }$ となります。

これを踏まえて、以下で、垂線のひき方を考えてみましょう。

垂線をひく方法

次のような、点 $\mathrm{P}$ と直線 $\ell$ があったとします。点 $\mathrm{P}$ は直線 $\ell$ 上にはない点です。

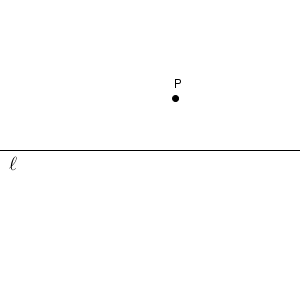
ここで、点 $\mathrm{P}$ を通り、直線 $\ell$ に垂直な直線をひく方法を考えてみましょう。【基本】作図で使う定規とコンパスで見たように、使っていい道具は定規とコンパスだけです。三角定規の90度の部分などを使わずに考えましょう。

直線をひくためには、通る2点がわかればいいですね。今の場合は、点 $\mathrm{P}$ を通る直線をかくので、もう1点、他にどの点を通るかがわかればいいです。垂直な直線は先ほどの図でもあらわれていましたが、これを利用して今の図と重ねて考えてみましょう。

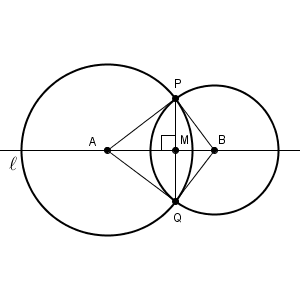
この図を見ると、直線 $\ell$ に垂直な線をひくためには、2つの直線の交点（上の図だと点$\mathrm{M}$）か、2つの円の交点（上の図だと点 $\mathrm{Q}$）のどちらかがわかるとよさそうですね。ところで、この2つの円はどうやってかけばいいんでしょうか。

円の中心は、どちらも直線 $\ell$ 上の点にする必要がありそうです。これらを中心として円をかくことにより、できあがった図は直線 $\ell$ について線対称となるからです。

一方、円の半径については、特に制限はありません。円の中心と点 $\mathrm{P}$ との距離が半径となりますが、半径が大きくても小さくても線対称であることに変わりはなく、 $\angle \mathrm{ AMP }$ と $\angle \mathrm{ AMQ }$ がぴったり重なること、どちらも90度であることには変わりはありません。実際、右側の円の半径をいろいろ変えてみても、 $\mathrm{ AB }\perp\mathrm{ PQ }$ であることがわかります。

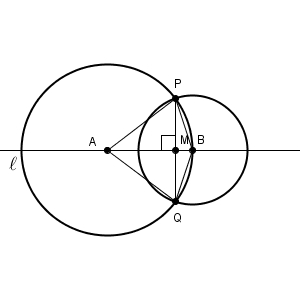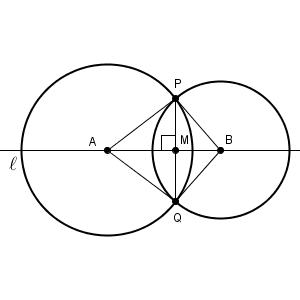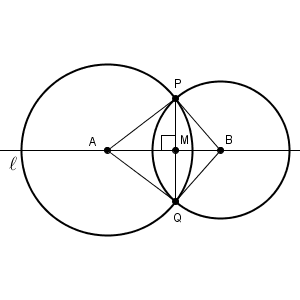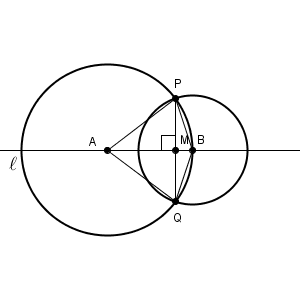
つまり、2つの円は、どちらも、直線 $\ell$ 上にとった点を中心として、その点から点 $\mathrm{P}$ までの距離を半径とする円であればいいことがわかります。これならコンパスだけで作図することができます。

2つの円をかくと交点が2つできるので、その交点を結ぶと直線 $\ell$ に垂直な線ができあがります。

以上から、「点 $\mathrm{P}$ を通り、直線 $\ell$ に垂直な直線」は、次のような手順でかくことができます。

1. STEP.1
   2点をとる
   直線 $\ell$ 上に2つの点をとる
2. STEP.2
   2つの円をかく
   選んだ2点のそれぞれを中心とし、点 $\mathrm{P}$ を通る円をかく
3. STEP.3
   垂線をひく
   2つの円の交点を結ぶ

実際には、円全体ではなく、次のような円の一部（つまり、弧）だけをかくことがほとんどです。

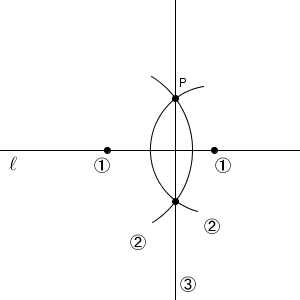
先ほどのStepと丸数字が対応しています。

こうして、ある点を通り、ある直線に垂直な直線をひくことができました。

おわりに

ここでは、ある点から、ある直線に垂線をひく方法を見てきました。線対称の性質を利用しました。作図する方法は他にもありますが、それは別のページで見ることにします。