【基本】垂線の作図(直線上にない点を通る)その2
ここでは、ある点からある直線へ垂線をひく方法を見ていきます。【基本】垂線の作図(直線上にない点を通る)その1で見た内容とは異なる作図の方法を見ていきます。
垂線の作図(直線上にない点を通る)その1の復習
次のような、点 $\mathrm{P}$ と直線 $\ell$ があったとします。点 $\mathrm{P}$ は直線 $\ell$ 上にはない点です。
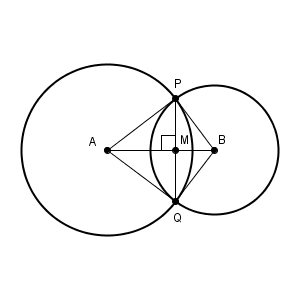
このページでも、点 $\mathrm{P}$ を通り、直線 $\ell$ に垂直な直線をひく方法を考えてみます。【基本】垂線の作図(直線上にない点を通る)その1では、2つの円を組み合わせた、次の図を利用しました。
上の図を参考に、①直線 $\ell$ 上に2つの点をとり、②点 $\mathrm{P}$ を通るように2つの円をかけば、点 $\mathrm{P}$ 以外にもう1つ交点ができます。直線 $\ell$ が対称の軸となることから、③2つの円の交点を結ぶと、直線 $\ell$ に垂直な直線が得られます。作図手順に番号をつけてかくと、次のような図になります。
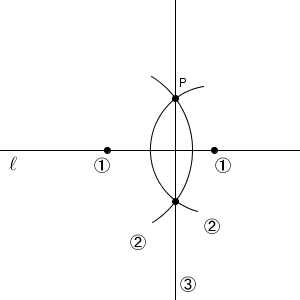
2つの円の交点がわかればいいので、②では、円全体ではなく、円の一部(つまり、弧)だけをかいています。
これが、垂線をひく作図方法の1つですが、もう1つよく知られている方法があります。以下で、見ていきましょう。
垂線の作図(直線上にない点を通る)その2
さて、同じ状況で、別の方法を考えます。

上の図で、点 $\mathrm{P}$ を通り、直線 $\ell$ に垂直な直線をひく方法を考えてみます。もう1つの方法でも、利用するのは2つの円を組み合わせた、線対称な次の図形です。

ただ、今回は少し見方を変えて利用します。先ほど復習した1つ目の方法では、直線 $\mathrm{AB}$ が直線 $\ell$ のことだと考えて作図しました。今回は、直線 $\mathrm{PQ}$ のほうを直線 $\ell$ のことだと思って作図してみます。上の図を、そのまま90度回転してみましょう。文字はいったん消してみます。
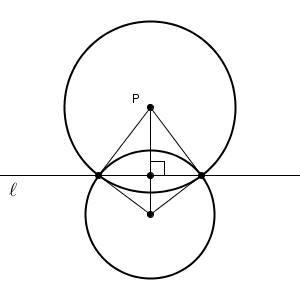
どうでしょうか。今考えている状況では、上の図の何がわかっていて、何を作図しないといけないでしょうか。
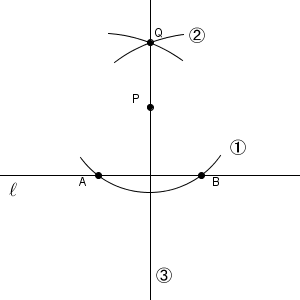
今回は、点 $\mathrm{P}$ が上側の円の中心だ、と考えます。そして、直線 $\ell$ 上に、2つの円の交点がある、という状況を考えます。この2点を結んでできる弦に垂直な直線が作図したい直線ですが、この直線をひくためには、下側の円の中心がどこかを特定できればいいですね。
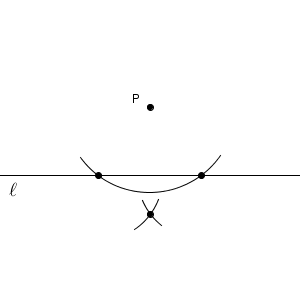
ここまでのことを踏まえて、次のように作図を行っていきます。まず、直線 $\ell$ 上に、2つの円の交点がくるような状況を考えます。これは、点 $\mathrm{P}$ を中心とした円をかきましょう。半径は、直線 $\ell$ と2点で交わるなら、どんな長さでもいいです。
交点がわかればいいので、円全体ではなく円の一部だけをかいています。あとは、下側の円の中心がどこかがわかればいいのですが、それは簡単にはわからないですね。そこで、考え方を変えて、「2つの交点から同じ距離だけ離れている点」と言い換えます。その点は、「2つの交点を通る円の中心」となります。
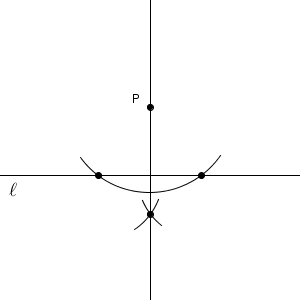
こうして、この交点と点 $\mathrm{P}$ とを結べば、直線 $\ell$ に垂直な直線ができます。
この方法でどうしてうまくいくのか、点に名前を入れて、もう少し考えてみましょう。
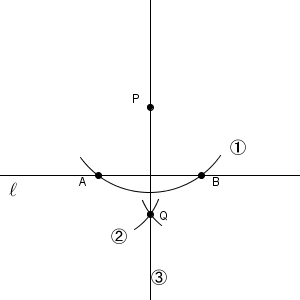
点 $\mathrm{P}$ を中心とした円をかいて、それと直線 $\ell$ との交点を $\mathrm{A, B}$ とすると、 $\triangle \mathrm{ ABP }$ は二等辺三角形となりますね。さらに、点 $\mathrm{A, B}$ から同じ半径の円をかいて交点を $\mathrm{Q}$ とすれば、 $\triangle \mathrm{ ABQ }$ も二等辺三角形です。
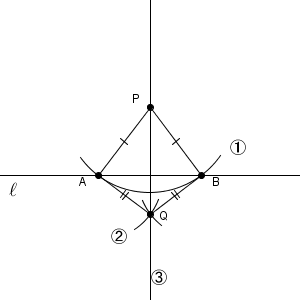
そのため、四角形 $\mathrm{APBQ}$ は、直線 $\mathrm{PQ}$ について線対称であることがわかります。直線 $\mathrm{PQ}$ で折ると、ぴったり重なるからですね。こうして、直線 $\mathrm{PQ}$ と直線 $\mathrm{AB}$ は垂直に交わることがわかります。
$\mathrm{ AP=BP }$ と $\mathrm{ AQ=BQ }$ はどちらも必要な条件ですが、 $\mathrm{AP}$ と $\mathrm{AQ}$ の長さは同じでなくても構いません(同じ長さにすることが多いですが)。さらにいうと、直線 $\ell$ から見て、点 $\mathrm{Q}$ を点 $\mathrm{P}$ と同じ側にとっても構いません(もちろん、このときは、点 $\mathrm{Q}$ は点 $\mathrm{P}$ と異なるようにとる必要はあります)。
ここでの作図方法では、直線 $\mathrm{PQ}$ が対称の軸となるようにすることを利用しているため、それが守られている限りは、正しく作図できます。
最後に、「点 $\mathrm{P}$ を通り、直線 $\ell$ に垂直な直線」のかきかたをまとめておきましょう。
- STEP.1直線上に2点を作図する点 $\mathrm{P}$ を中心として、直線 $\ell$ と2点で交わる円をかく
- STEP.2交点からの距離が等しい点を作図する2つの交点を中心とし、同じ半径の円をかいて、交点を作る
- STEP.3垂線をひく先ほどの交点と点 $\mathrm{P}$ とを結ぶ
おわりに
ここでは、直線上にない点からある直線に垂直な線をひく作図方法を見てきました。2つの円の中心を求める、という発想で作図しました。2つの作図方法を見てきましたが、指定がなければどちらで作図をしても構いません。