【基本】点と直線
ここでは、図形を考えていく上で基本となる、点や直線に関する用語を見ていきます。
点
中学の数学の世界では、図形の性質をいろいろ見ていくことになりますが、その前に、いろいろな用語を見ていくことにしましょう。すでに見たり聞いたりしたことがあるものが多いと思います。
まずは、点(point) です。点とは、ある1つの場所を表すものです。位置だけを表すもので、理論上は、大きさを持ちません。

「大きさを持たない」といっても、それでは人間の目にはどこにあるのか見えません。そこで、実際には、便宜上、上のように少し塗りつぶして表現します。ただ、あくまでも、「本当は、点は大きさを持たない」ということは知っておきましょう。
複数の点を扱う場合、どの点のことを言ってるのかわからなくなってしまうので、点に名前をつけて呼ぶことがあります。点$\mathrm{A}$ とか点$\mathrm{P}$ などと呼びます。
線分と直線
2点$\mathrm{A, B}$ を通るまっすぐな線は、次のように一本だけ引くことができます。
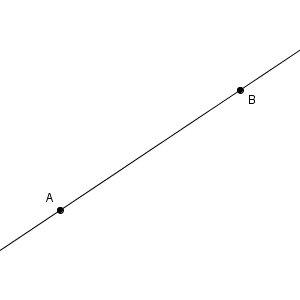
このように、まっすぐで、どちらの方向にもずっと伸びている線のことを直線(line) といいます。2点$\mathrm{A, B}$ を通る直線は、直線$\mathrm{AB}$ といいます。直線$\mathrm{BA}$ と言っても同じ直線を指しますが、アルファベット順で書くことが多いです。また、通る点を書かずに、単に名前だけを付けたい場合は、直線 $\ell$, 直線 $m$ などと呼ぶこともあります。
場合によっては、2点の間の部分だけを考えたいときもあります。
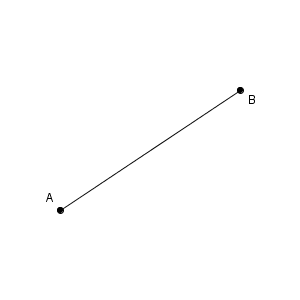
このように、2点を結ぶ直線のうち、2点の間と両端を合わせた部分を、線分(line segment) といいます。2点$\mathrm{A, B}$ が両端となっている線分のことを、線分$\mathrm{AB}$ といいます。線分$\mathrm{BA}$ と呼んでも構いません。同じものを指します。
直線は両サイドに伸びていて、線分はどちらにも伸びてはいませんが、この中間にあたる図形もあります。
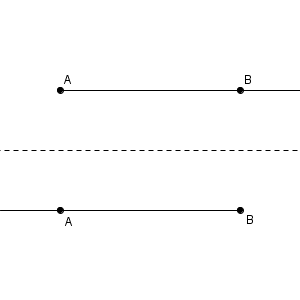
片方は伸びてなくて、もう片方は伸びている、という線です。このような線を、半直線(half line) といいます。半直線$\mathrm{AB}$ というと、上の1つ目のように、点$\mathrm{A}$ から出発して、点$\mathrm{B}$ のほうにずっと伸びていく線を指します。一方、半直線$\mathrm{BA}$ は、点$\mathrm{B}$ から出発して、点$\mathrm{A}$ のほうにずっと伸びていく線を指します。半直線の場合は、$\mathrm{AB}$ と $\mathrm{BA}$ で内容が異なるので注意しましょう。
直線、線分、半直線は、いずれも、幅を持ちません。ただ、それだと、人間の目には見えないので、幅のある線でかきます。
2点間の距離
線分$\mathrm{AB}$ の長さのことを、2点$\mathrm{A, B}$ 間の距離(distance) といいます。
2点間の距離は、片方の点からもう片方の点へ移動するときに、移動距離が一番短くなるときの長さを表している、ともいえます。
線分$\mathrm{AB}$ の長さと線分$\mathrm{CD}$ の長さが等しいとき、式で\[ \mathrm{ AB=CD } \]と表します。
下の図は、 $\mathrm{AB=AC}$ の三角形です。
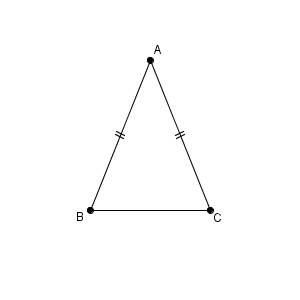
図では、同じ記号を用いて、2つの線分の長さが等しいことを示す場合があります。
なお、あまり多くはないですが、参考書によっては、線分 $\mathrm{AB}$ の長さを、絶対値の記号を使って $|\mathrm{ AB }|$ と書いていることもあります。
平行
2つの直線$\mathrm{AB}$, $\mathrm{CD}$ が交点を持たないとき、2つの直線は平行(parallel) である、といいます。また、2直線$\mathrm{AB}$, $\mathrm{CD}$ が平行であるとき、2つの線分$\mathrm{AB, CD}$ も平行である、といいます。
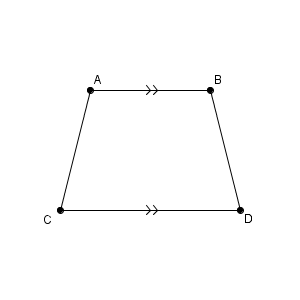
2つの直線が平行であることを、図の中で、「>」や「>>」という記号を用いて表すことがあります。
また、2直線$\mathrm{AB, CD}$ が平行であることは、式で\[ \mathrm{ AB /\!/ CD } \]と表します。
おわりに
ここでは、点や直線、線分などに関連する用語をまとめてきました。ほとんどは見聞きしたことがあると思いますが、いくつか初めて出てくる項目もあったかもしれないですね。今後、図形の内容を学んでいく上で、何の説明もなく出てくるものもあるので、覚えておきましょう。