【基本】正負の数と大小
ここでは、正の数と負の数に対する大小関係について考えていきます。
不等号で大小を表そう
【基本】符号のついた数で見たように、 $0$ より大きな数を正の数、 $0$ より小さな数を負の数というのでした。
このように、2つの数を比べて、「より大きい」とか「より小さい」ということを、「 $\gt$ 」や「 $\lt$ 」といった記号で表します。これらを、不等号(sign of inequality) といいます。「 $\gt$ 」は、「大なり」と読み、「 $\lt$ 」は、「小なり」と読みます。どちらも、広がっている方が、大きい数であることを表します。
例えば、 $+1$ は $0$ よりも $1$ だけ大きな数だから、 $+1$ のほうが大きいので、\[ +1 \gt 0 \]と表すことができます。一方、 $-3$ は、 $0$ よりも $3$ だけ小さな数なので、 $0$ のほうが大きいですね。なので、\[ -3\lt 0 \]と表せます。
それでは、正の数と負の数を比べたときや、正の数同士、負の数同士を比べたときにはどうなるでしょうか。これらの場合に、どちらが大きいかを考えるために、図を使って考えてみます。
負の数を含めた数直線を考えよう
数の大小を考えるために、図を使って考えることにしましょう。直線をかいて、各点と数とを対応させてみます。
まず、左右に伸びる直線をかきます。そして、適当な場所に(普通は真ん中くらいに)、 $0$ を対応させることにしましょう。
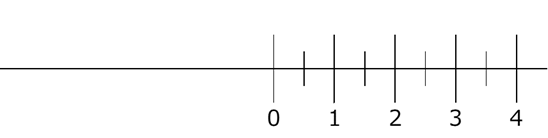
次に、右に $+1$ に対応する点をとります。一般的に、数学の世界では、 $+1$ の場所は $0$ の右側にとります。
そして、順番に、 $+2$, $+3$ と数を記入していきます。右に行くほど大きな数になります。(下の図では、間の $0.5$ にも目盛りを入れています)
また、左側は、基準から反対側に移動していくので、負の数を対応させます。【基本】符号のついた数では、大きい・小さい、高い・低い、多い・少ない、といった量を、正の数・負の数を使って表しましたが、このように反対の性質を持つものは、正の数と負の数で表せるのでした。なので、左側の点に負の数を対応させるのは自然でしょう。
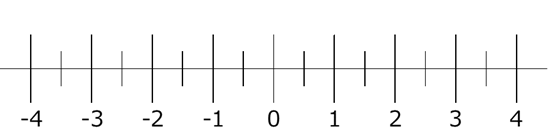
このように、 $-1$, $-2$, $-3$ と記入していきます。左に行くほど、小さな数になります。
一般に、このように、各点と数とを対応させた直線のことを、数直線(number line) といいます。数直線は、ここで見たように、普通は左右に伸びる直線を使い、右に行くほど大きな数となるようにします。
例えば、 $+1$, $-3$, $-1.5$, $\dfrac{1}{2}$ に対応する点を考えると、次のようになります。

右に行くほど大きな数になるので、この4つの数の中では、 $+1$ が一番大きく、あとは $\dfrac{1}{2}$, $-1.5$, $-3$ と続きます。これを不等号を使って表せば、\[ +1 \gt \dfrac{1}{2} \gt -1.5 \gt -3 \]となります。もちろん。\[ -3 \lt -1.5 \lt \dfrac{1}{2} \lt +1 \]でもかまいません。
このように、不等号は複数個を同時に使うこともあります。ただ、その場合には、不等号の向きは同じにしないといけません。例えば、 $+1\gt -3 \lt -1.5$ といった書き方はしません。この書き方だと、 $+1$ と $-1.5$ のどちらが大きいか、わからないからです。
数直線で、 $0$ に対応する点を原点といいます。また、 $0$ から見れば、右側に正の数、左側に負の数があるので、右の方向を正の方向といい、左の方向を負の方向といいます。
数直線を使って考えてみましょう。
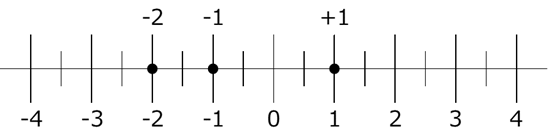
小さい順番に書くと、\[ -2 \lt -1 \lt +1 \]となります。これが答えです。
おわりに
ここでは、正負の数の大小を考えてきました。数直線を使って書けば、簡単に考えることができますが、毎回数直線をかくのは面倒ですね。数直線をかかなくても考える方法は、【基本】絶対値と数と大小で見ていくことにします。