【基本】対称移動(東京オリンピックエンブレムを利用)
ここでは、対称移動について見ていきます。
東京オリンピックエンブレムと対称移動
ここでも、東京2020オリンピック・パラリンピックのエンブレムを見ながら、図形の移動について考えていきます。

右側のパラリンピック用のエンブレムは、左右対称になっています。つまり、中央の線について折り返せば、ぴったりと重なります。

図形をある直線を折り目として折り返す移動のことを、対称移動(reflection) といいます。このときに折り目となる直線のことを、対称の軸といいます。対称の軸のところに鏡を置いたと考えるとわかりやすいかもしれません。
また、上のパラリンピックエンブレムのように、対称移動をしたときに元の図形にぴったりと重なるような図形を、線対称な図形といいます。
対称移動の性質
回転移動のときと同じように、対称移動についても、移動の前後で対応する点がどのように移動するかを見てみましょう。

上の図のように、三角形 $\mathrm{ABC}$ を直線 $\ell$ について対称移動したときに、三角形 $\mathrm{DEF}$ に移ったとします。このとき、対応する点を線分で結ぶと、次のようになります。
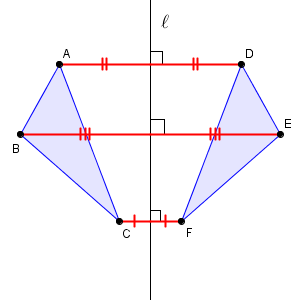
対応する点は、直線 $\ell$ で折り返すとぴったりと重なることから、直線 $\ell$ は対応する2点の中点を通り、対応する点を結んだ線分は直線 $\ell$ と垂直に交わることがわかります。言い換えると、対応する2点を結んだ線分の垂直二等分線が直線 $\ell$ になっている、ということもできます。
垂直二等分線の作図方法は、【基本】垂線二等分線の作図などで見ました。そのため、今後は、対称移動した後の図形を作図するような問題も解いていくことになります。
例題
ここでは、コンパスを使わずに作図できる問題を見ていきます。
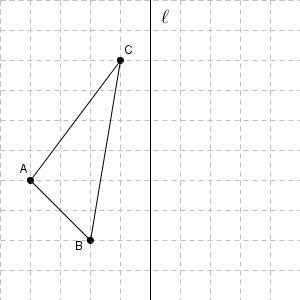
対称移動によって、各頂点がどのように移動するかを考えてみましょう。直線について反対側に移動するので、例えば点 $\mathrm{A}$ であれば、直線から右側へ同じだけ離れた点に移動することがわかります。ほかの点も同様に考えれば、次のようになることがわかります。

このように、マス目が入っていて、対称の軸がマス目にそっている場合は、コンパスを使わずに移動後の図形をかくことができます。
おわりに
ここでは、対称移動について見てきました。対称の軸を折り目として折り返すように移動することを言うのでした。対応する2点を結ぶと、対称の軸が垂直二等分線になっている点もおさえておきましょう。