【基本】図形の移動と合同
ここでは、図形の移動と形や大きさに関する関係について見ていきます。
図形の移動前後での図形の変化
図形の移動について、3種類の移動を見てきました。平行移動、回転移動、対称移動の3つです。
これらの移動は、図形全体を、向きを変えずにずらす、回転させる、折り返す、といった移動なので、もとの図形が変わってしまうことはありません。そのため、これらを組み合わせて移動した場合、移動前と移動後の図形は、大きさも形も同じになります。このように、2つの図形が、大きさも形も同じであるとき、2つの図形は合同である(congruent) といいます。言い換えると、ピッタリと重ね合わせることができれば、合同だということです。
ある図形を、平行移動、回転移動、対称移動を組み合わせて移動すると、移動前と移動後の図形は合同になりますが、実は、これの逆のこともいえます。つまり、2つの図形が合同である(ピッタリと重ね合わせることができる)ならば、平行移動・回転移動・対称移動を組み合わせることで、片方の図形をもう片方の図形に移動させることができます。以下で、具体的な例を用いて考えてみます。
下の図のように、2つの合同な三角形があったとします。

まずは、対応する1つの頂点が重なるように平行移動します。

次に、もう1つの頂点のペアを重ねます。先ほど重なった頂点を中心として回転させます。結果的に2組の頂点が重なるようになります。
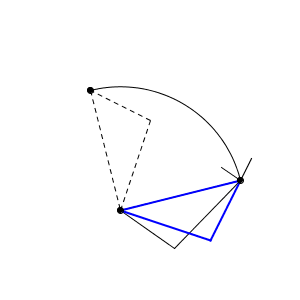
2つの三角形は合同なので、上のように移動すれば、対応する辺はピッタリと重なります。残りの頂点は、対称移動を繰り返して重ねることができます。
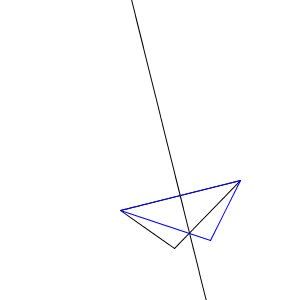
重なった辺が対称の軸となることもありますし、その辺の垂直二等分線が対称の軸となることもあります。こうして3つの頂点はピッタリと重なります。
他の場合であっても、平行移動で1つの頂点を合わせる(基準の位置をそろえる)、回転移動で1つの辺を合わせる(向きをそろえる)、対称移動で残りの辺を合わせる(表裏をそろえる)を組み合わせて、2つの合同な図形を移動によってピッタリと重ねることができます。
例題
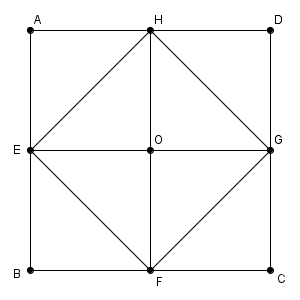
(1) 三角形 $\mathrm{AEH}$ を三角形 $\mathrm{OFG}$ に重ねるには、どのように移動させればいいか、1つ挙げなさい。(頂点の対応は考えなくてもよい。例えば、$\mathrm{E}$ が $\mathrm{F}$ に重ならずに $\mathrm{G}$ に重なってもよい。以下の問題も同様。)
(2) 三角形 $\mathrm{EBF}$ を三角形 $\mathrm{OFG}$ に重ねるには、どのように移動させればいいか、1つ挙げなさい。
(3) 三角形 $\mathrm{HEO}$ を三角形 $\mathrm{OFG}$ に重ねるには、どのように移動させればいいか、1つ挙げなさい。
平行移動、回転移動、対称移動を組み合わせて試行錯誤しましょう。答えは一つではなく、いろいろな方法があります。
どの三角形も、直角二等辺三角形なので、長さの等しい2辺は、どのように重ねても構いません。ただ、それだと自由度が高いので、直角の部分や斜辺を重ねることを考えたほうがわかりやすいかもしれません。

(1)は、三角形 $\mathrm{ AEH }$ を移動して、三角形 $\mathrm{OFG}$ に重ねる方法です。これは、単純にスライドさせればいいですね。点 $\mathrm{A}$ が点 $\mathrm{O}$ に重なるように平行移動すれば、他の頂点も重なり、三角形同士が重なることがわかります。
(2)は、三角形 $\mathrm{EBF}$ を移動する問題です。これは、平行移動しても重なりません。点 $\mathrm{F}$ 同士はすでに重なっているので、他の頂点が重なるように移動するには、回転移動を使う方法があります。点 $\mathrm{F}$ を中心に、時計回りに90度回転すれば、$\mathrm{B}$ が $\mathrm{O}$ に、 $\mathrm{E}$ が $\mathrm{G}$ に重なります。
(3)は、三角形 $\mathrm{HEO}$ を移動する問題です。先ほどと同じように回転移動を使って重ねることができます。点 $\mathrm{O}$ を中心として、180度回転すれば、三角形 $\mathrm{HEO}$ は三角形 $\mathrm{OFG}$ に重なります。
対称移動を使う方法もあります。直線 $\mathrm{BD}$ を軸として対称移動すると、三角形 $\mathrm{HEO}$ は三角形 $\mathrm{OFG}$ に重ねることができます。

この問題では、3種類の移動を組み合わせることはありませんでしたが、組み合わせて移動することも可能です。例えば、(3)であれば、$\mathrm{O}$ が $\mathrm{C}$ に重なるように平行移動すると、三角形 $\mathrm{HEO}$ は三角形 $\mathrm{GFC}$ に重なります。それから、直線 $\mathrm{FG}$ を軸に対称移動すれば、三角形 $\mathrm{OFG}$ に重ねることができます。
また、(2)では、三角形 $\mathrm{EBF}$ を、直線 $\mathrm{EF}$ について対称移動し、さらに、直線 $\mathrm{FG}$ について対称移動させることで、三角形 $\mathrm{OFG}$ に重ねることもできます。
おわりに
ここでは、平行移動、回転移動、対称移動によって、図形の形や大きさが変わらないことを見ました。また、形も大きさも同じであれば、2つの図形は3種類の移動を組み合わせてピッタリ重ねることができる、ということも見ました。このことから、この3つの移動が大事であることがわかります。
なお、合同については、将来、さらに詳しく見ていくことになります。