【基本】作図で使う定規とコンパス
ここでは、作図を行うときに使う道具や使い方のルールについて説明していきます。
作図
これから、いろいろな図形をかく方法について学んでいきます。図形をかくことを、作図(construction) といいます。
数学での作図では、使う道具が限られていたり、やっていいこととやってはいけないことが決められていたりします。以下で、説明していきます。
定規
作図で使う道具の1つに、定規(ruler) があります。

作図では、定規はまっすぐな線を引くことに使います。「そりゃそうだ」と思うかもしれませんが、重要なのはここからです。定規はまっすぐな線を引く以外に使うことはできません。
例えば、普通、定規には目盛りがついているはずですが、この目盛りを使って長さを測って作図をすることはできません。実生活では、もちろん長さを測ることに使ってもいいのですが、数学の作図ではそのような使い方は許されていません。
また、上のような三角定規を使う場合、30度、45度、60度、90度が含まれていることがありますが、これらを作図で利用することもできません。ここの角を使って角度を測ったり、垂直な線を引くためにこれらの角を利用することはできません。
さらに、2つの定規を組み合わせて作図をすることもできません。片方を固定し、もう片方をスライドさせて平行な線を引く、という使い方はできません。
せっかく便利な機能があるのに、わざわざ使わないのはもったいない気がしますね。ただ、数学での作図では、指定された図形がかくことが目的なのではなく、いろいろな図形の性質を理解したり応用したりするのが目的なんですね。なので、このような制限がついています。今までも、長さや角度を求める問題では、定規や分度器を使いませんでしたが、それと似たような理由です。
定規は、まっすぐな線を引くことに使います。好きな直線を引いてもいいし、ある1点を通る好きな直線を引いてもいいし、2つの点を結んだり、線分を伸ばして直線にしてもいいのですが、それ以外はできません。特別に指定されていない限りは、このルールで作図します。
コンパス
作図では、コンパス(compass) も使うことができます。

コンパスは、主に、円をかくために使います。針の部分を円の中心に定めて固定し、鉛筆の部分をくるっと動かせば、円をかくことができます。円全体ではなく、円の一部(つまり、弧)だけでも構いません。
針と鉛筆の部分が半径になるわけですが、この半径は、好きな長さにすることもできますし、すでに作図されている2点間の長さをとることもできます。
一番シンプルな例は、「点 $\mathrm{A}$ を中心とし、点 $\mathrm{B}$ を通る円」です。このときは、針の部分を点 $\mathrm{A}$ に定め、鉛筆の部分を点 $\mathrm{B}$ に定めて円をかくことができます。
また、図の中に、点 $\mathrm{A, B, C}$ があって、点 $\mathrm{A}$ が中心で、半径が線分 $\mathrm{BC}$ の長さとなる円もかくことができます。コンパスの針と鉛筆の距離を、点 $\mathrm{B, C}$ にそれぞれ合わせ、その距離を保ったまま、点 $\mathrm{A}$ を中心に円をかくことができます。このような、2点間の長さをとることはできます。
しかし、決まっていない長さを目分量でとることはできません。例えば、中心がどこかわかっていない円があったとして、「中心は大体このあたりだろう、そうすると半径はこのくらいだな」というような感じで長さをとることはできません。作図されている2点間の長さはとれますが、作図していないものはとれません。
他の道具
数学の作図で使える道具は、定規とコンパスだけで、それ以外は使えません。分度器は使えないので、角度を測って作図することはできません。
うーん、でも本当に定規とコンパスだけでいろいろ作図できるんでしょうか。さすがに、角度に関するものはかけないんじゃないか。そう思うかもしれないので、簡単な作図を一つやってみましょう。定規とコンパスだけで、60度を作ってみましょう。
まずは、定規を使って適当に直線を引いて、適当な2点をとります。点 $\mathrm{A, B}$ と置いてみましょう。
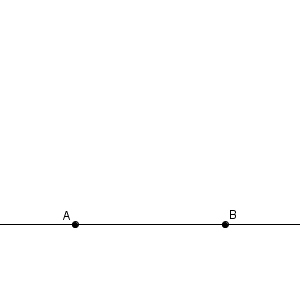
次に、点 $\mathrm{A}$ を中心として半径が線分 $\mathrm{AB}$ と同じ長さの円の一部をかきます。
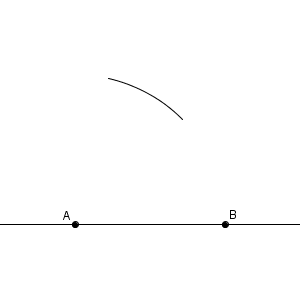
続いて、点 $\mathrm{B}$ を中心として半径が線分 $\mathrm{AB}$ と同じ長さの円の一部をかきます。先ほどかいたものと交わるように調整し、交点を $\mathrm{C}$ としましょう。
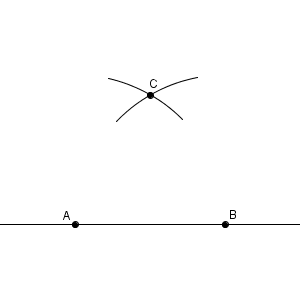
このとき、線分 $\mathrm{AB}$, $\mathrm{BC}$, $\mathrm{CA}$ は、すべて線分 $\mathrm{AB}$ と同じ長さです。どれも円の半径で、2つの円の半径は線分 $\mathrm{AB}$ の長さでかいたからですね。なので、三角形 $\mathrm{ABC}$ は正三角形だから、 $\angle \mathrm{ CAB }$ は60度となります。
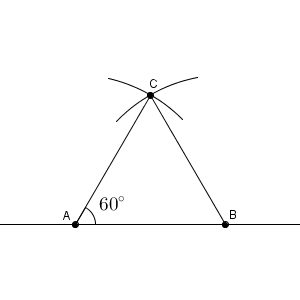
こうして、分度器を使わなくても、定規とコンパスだけで60度を作り出すことができました。作図の問題では、単に図をかくだけでなく、どのようにかいたかも重要です。なので、作図する際に用いた線は、消さずにそのまま残しておきます。
今後は、このようにして、定規とコンパスを組み合わせるだけで、いろいろな図形をかいていく方法を学んでいくことになります。
おわりに
ここでは、作図に使う定規とコンパスについての説明をしてきました。また、作図のルールも説明してきました。定規は、直線を引くために使います。コンパスは主に円をかくために使いますが、2点間の長さをとることに使うこともあります。これらのルールを守りつつ、今後はいろいろな図形のかき方を学んでいきます。