【基本】平行移動(東京オリンピックエンブレムを利用)
ここでは、平行移動について見ていきます。
東京オリンピックエンブレムと図形の移動
東京2020オリンピック・パラリンピックでは、次のようなエンブレムが使われていました。エンブレムとは、シンボルマークのようなものです。

左側がオリンピック用で、右側がパラリンピック用です。
二つのエンブレムは、全体を見ると円形に並んでいるように見えますが、各パーツは3種類の四角形で構成されています。正方形、太い長方形、細長い長方形の3つです。この3つの異なる四角形は「多様性」を表しており、円は「調和」を表している、と言われています。
3種類の四角形は、左右で同じ枚数が使われています。どちらも、正方形は9枚、太い長方形は18枚、細長い長方形は18枚使われています(数えてみましょう)。
ただ、もっとよく見ると、枚数が同じだけではありません。向きも同じです。例えば、左側のエンブレムで正方形の数を数えれば気づくかもしれませんが、正方形の向きが違うものがあります。まっすぐなもの、少し左に傾いているもの、少し右に傾いているもの、それぞれ3つずつあります。そして、それらは右のエンブレムにも同じようにあります。
実は、左側のエンブレムで、それぞれの四角形の向きを変えずにずらしていくと、右側のエンブレムになることが知られています。下のツイートは、それを発見した人が作成した動画です。
枚数が同じどころじゃなかった。パーツごとの角度も変えないままオリンピックからパラリンピックにできる pic.twitter.com/TIv4IruvM8
— 鯵坂もっちょ🐟夏コミありがとうございました (@motcho_tw) April 26, 2016
オリンピックとパラリンピックのエンブレムが、このように対応しているのはすごいですね。
この移動のように、向きを変えずに移動することを 平行移動 といいます。次で、もう少し詳しく見ていきます。
平行移動
下の図のように、左側の三角形を右側の三角形へと動かす移動を考えてみましょう。

このように、向きを変えずに動かす移動は、先ほども見ましたね。
移動によって、対応する点はどのように移動するでしょうか。三角形の各頂点を線分でつないでみると、次のようになります。

それぞれの点は、同じ方向に、同じ距離だけ移動しています。そのため、上のように作った3つの線分は、互いに平行で、同じ長さになります。「対応する点を結ぶと平行な線分ができる」ことから、このような移動を、平行移動(translation) といいます。
はじめのほうでは、「向きを変えずに動かす」と説明していました。イメージとしては「図形の向き」はわかるかもしれませんが、厳密には説明していません。そのため、ここでは、「図形全体を、ある方向に、ある距離だけ動かす」という説明を採用しています。
例題
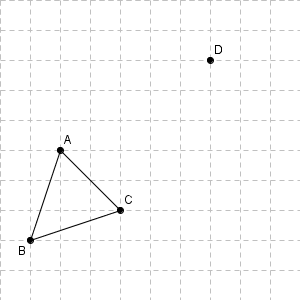
同じ向きに同じ長さだけ平行移動させればいいです。点 $\mathrm{A}$ から点 $\mathrm{D}$ に移動するには、右に $5$ 移動し、上に $3$ 移動すればいいので、点 $\mathrm{B, C}$ も同じように移動すれば、点 $\mathrm{E, F}$ が得られます。
以上から、次のようになります。

おわりに
ここでは、平行移動について見てきました。対応する点を結ぶと平行な線分が出てくることから、平行移動という名前がついています。