【基本】文字を使った式で表そう
ここでは、マッチ棒で正方形を作る問題を利用して、文字を使う方法を見ていきます。
正方形を作るのにマッチ棒は何本必要か
同じ長さのマッチ棒がたくさんあるとして、次のように正方形を作るとしましょう。

縦の長さが、マッチ棒1本分の長さです。上の図では、正方形が4つできています。このように、横に横に正方形を作っていったとき、正方形を10個作るには、マッチ棒は何本必要でしょうか。
正方形を実際に10個作り、直接数えても答えは出せます。しかし、それは面倒だし、数え間違いが起きそうですね。なので、規則性を考えてみましょう。正方形が増えるごとに、マッチ棒がどのように増えていくかがわかれば、直接数えなくても、計算で求めることができそうですね。
規則性を考えるために、正方形が少ないケースをいくつか考えてみましょう。
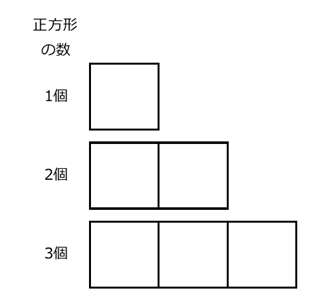
正方形の数もマッチ棒の数も少ないので、これなら直接数えるのも大変ではないですね。正方形の数とマッチ棒の数の対応は、次のようになっています。
| 正方形の数 | マッチ棒の数 |
|---|---|
| 1個 | 4本 |
| 2個 | 7本 |
| 3個 | 10本 |

正方形が1つ増えることによって、どこが変化しているかに注目しましょう。すると、右端の正方形を作るために、マッチ棒が3本が増えていることに気づくでしょう。そのため、次のように、3本ずつまとめてみます。
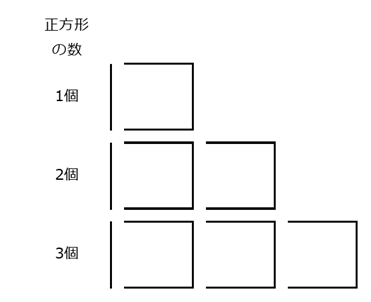
こうすると、例えば、正方形が2個の場合、マッチ棒の構成は、左端の「|」が1つと、その右側の「コ」の形2つが並んでいる、と考えることができます。このことから、正方形が2つの場合に必要なマッチ棒の数は
1+3×2
と表せることがわかります。この式の、1は左端にある「|」を表していて、その次の3は「コ」の部分を表しています。そして、最後の2が、「コ」の数を表しています。「コ」の数と正方形の数は同じですね。なので、正方形が10個の場合なら、上の式の2を10に変えればよく、
1+3×10
と表せることがわかります。こうして、正方形10個を作るのに必要なマッチ棒の本数は31本とわかります。
文字を使って表そう
引き続き、先ほどのマッチ棒の問題を考えてみましょう。

先ほどの内容から、正方形を10個作る場合、「|」を1組、「コ」を10組作ればいいので、
1+3×10
本のマッチ棒が必要であることがわかりました。同じように考えれば、正方形が20個なら「1+3×20」本となり、正方形が100個なら「1+3×100」本となります。正方形がいくつであっても、正方形の数とマッチ棒の関係がわかっているので、簡単にマッチ棒の数を求めることができます。この関係を式で書くと、
1+3×(正方形の数)
となります。このような「言葉」(今の場合は、「正方形の数」)を使って式を書くと、何を表しているかはわかりやすい反面、式自体が長くなり、扱いにくいです。そのため、数学の世界では、このような言葉を、アルファベット1文字で置き換えて表現します。今の場合であれば、正方形の数を $x$ 個と表すことにすると、 $x$ 個の正方形を作るのに必要なマッチ棒の数は\[ 1+3\times x \]本になる、というように表現します。
この場合の $x$ は、1, 2, 3 や、10, 20, 100 といった、様々な数字をまとめて表しています。使う文字は、どんな文字でも構いません。また、文字が表す数字は、自然数に限らず、小数や負の数を表すこともあります。次の例題を通して、いろいろなケースを見てみましょう。
例題
(1) 太郎さんには3歳年上のお兄さんがいます。太郎さんが $x$ 歳のとき、お兄さんの年齢は何歳ですか。
(2) 1辺が $a$ cmの正方形の周の長さは、何cmですか。
(3) 昨日の最高気温が $t$ ℃で、今日の最高気温は昨日より3℃低くなりました。今日の最高気温は何℃ですか。
(1)は、太郎さんの年齢に3を足せばお兄さんの年齢になります。太郎さんの年齢が $x$ 歳なので、お兄さんの年齢は $(x+3)$ 歳となります。
(2)は、1辺の長さを4倍すれば、正方形の周の長さになります。1辺の長さが $a$ cmなので、正方形の周の長さは $(a\times 4)$ cmとなります。
(3)は、昨日の最高気温から3を引けば、今日の最高気温になります。昨日の最高気温が $t$ ℃なので、今日の最高気温は $(t-3)$ ℃となります。
(2)(3)のように、 $x$ 以外の文字が使われることもありますが、いろいろな数を表していることに変わりはありません。
(1)の場合、 $x$ は年齢なので、0以上の整数を表しています。(2)の場合は、 $a$ は1辺の長さなので、正の数を表しています。整数以外の数も表しています。(3)は、 $t$ は負の数も含めて表しています。このように、文字は、いろいろな数を表してはいますが、どのような数を表しているかは、状況によって異なります。
おわりに
ここでは、文字を使った式で表す方法について見てきました。これから、いろいろなものを文字を使った式で表していく方法を見ていくことになります。