【応用】最短経路の作図
ここでは、最短経路に関する作図について見ていきます。
最短経路の基本的な考え方
作図の問題の中には、最短経路を考える問題があります。例えば次のような図を見てみましょう。

点 $\mathrm{A}$ を出発し、直線 $\ell$ 上の点を通ってから、点 $\mathrm{B}$ へ移動するとします。このとき、移動距離が一番短くなるのは、直線 $\ell$ 上のどの点を通るときでしょうか。
点 $\mathrm{A}$ が今いる場所で、点 $\mathrm{B}$ が目的地、直線 $\ell$ が大きな道路だとすると、日常でも似たような問題を考えるシチュエーションはありそうです。どう移動するのが一番短くなるでしょうか。
このケースは簡単ですね。寄り道せずに、まっすぐ $\mathrm{A}$ から $\mathrm{B}$ まで移動するのが最短になります。
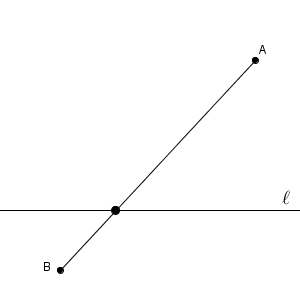
移動距離がこれより短くなることはありません。なので、直線 $\ell$ と線分 $\mathrm{AB}$ との交点を通ることがわかります。
このように、2点間の移動距離が最小になるのは、2点を線分で結んだとき となります。これが最短経路の問題のポイントとなります。
最短経路の問題その1
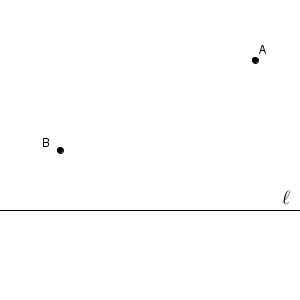
問題によっては、直線 $\ell$ が川であり、点 $\mathrm{A}$ を出発して川で水を汲んで点 $\mathrm{B}$ へ行くときの移動距離、などとなっていることもあります。
$\mathrm{A}$ から $\mathrm{P}$ まで、 $\mathrm{B}$ から $\mathrm{P}$ までの距離は、それぞれを線で結んだときの長さになります。しかし、 $\mathrm{P}$ が動けば、長さの和は変わってしまいます。
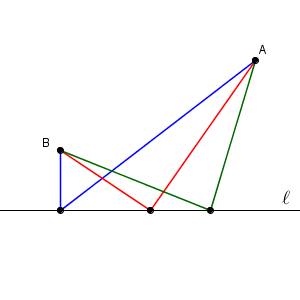
$\mathrm{A}$ から $\mathrm{B}$ まで行くだけなら、線分 $\mathrm{AB}$ を通るのが一番の近道ですが、今回はわざわざ直線 $\ell$ 上の点を通らないといけないのでやっかいですね。どのように作図すればいいでしょうか。
$\mathrm{A}$ から出発して直線 $\ell$ についた後で、点 $\mathrm{B}$ の方向へ折り返してしまうのでやっかいなんですね。もしまっすぐ行けたら簡単なのですが。
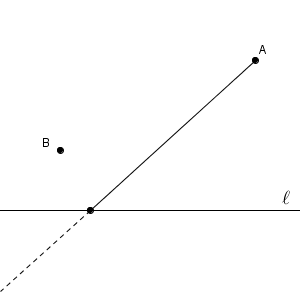
これは言われないとなかなか気づかないですが、直線 $\ell$ について点 $\mathrm{B}$ と対称な点を考えます。この点を $\mathrm{C}$ としましょう。すると、 $\mathrm{ BP=CP }$ となります。なので、 $\mathrm{ AP+BP }$ が最小になるのは、 $\mathrm{ AP+CP }$ が最小になるのと同じときです。
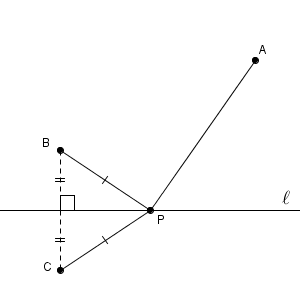
$\mathrm{ AP+CP }$ が最小になるときはいつか分かりますね。先ほどのポイントで見た通り、線分 $\mathrm{AC}$ と直線 $\ell$ との交点を $\mathrm{P}$ としたときが最小です。なので、 $\mathrm{ AP+BP }$ が最小になるときもこのときになります。
以上から、まず、直線 $\ell$ について点 $\mathrm{B}$ に対称な点を作図します。これができれば、点 $\mathrm{P}$ は簡単に作図できます。
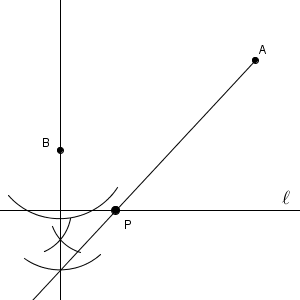
これが完成図ですが、点に名前をつけて手順を書いてみます。

まず、点 $\mathrm{B}$ から直線 $\ell$ への垂線をひきます。この垂線と直線 $\ell$ との交点を $\mathrm{M}$ とし、$\mathrm{M}$ が中心で半径が $\mathrm{BM}$ の円をかきます。この円と垂線との交点を $\mathrm{C}$ とします($\mathrm{B}$ ではないほうです)。この $\mathrm{C}$ が、直線 $\ell$ について、点 $\mathrm{B}$ に対称な点となります。
あとは、線分 $\mathrm{AC}$ と直線 $\ell$ との交点を作れば、これが点 $\mathrm{P}$ となります。これで完成です。
$\mathrm{ AP+BP }$ は考えにくいですが、同じ長さである $\mathrm{ AP+CP }$ を使えば、いつ最小になるかがわかりやすいですね。まっすぐな線で結べるように移動して考えます。
最短経路の問題その2

問題によっては、直線 $\ell,m$ の間が川で、どこに橋を掛ければ移動距離が最短になるか、などとなっていることもあります。
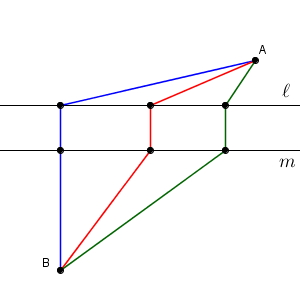
直線 $\ell.m$ が平行なので、線分 $\mathrm{PQ}$ の長さはつねに同じです。なので、 $\mathrm{ AP+QB }$ の長さを考えればいいです。これも先ほどと同じようにして、「2点間の移動距離が最小になるのは、2点を線分で結んだとき」が使えるように考えましょう。
今回は、 $\mathrm{ AP+QB }$ が途中で途切れている点がやっかいですね。まっすぐ行けたら簡単になるのですが。
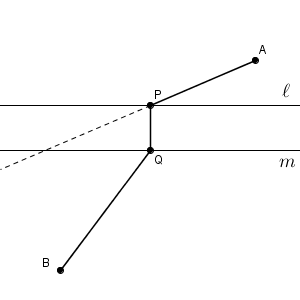
これも言われないとなかなか気づきにくいですが、点 $\mathrm{B}$ を上にスライドして考えます。直線 $\ell,m$ の距離の分だけ上にスライドした点を $\mathrm{C}$ とします。このとき、四角形 $\mathrm{BCPQ}$ は平行四辺形となります(厳密には証明が必要です)。
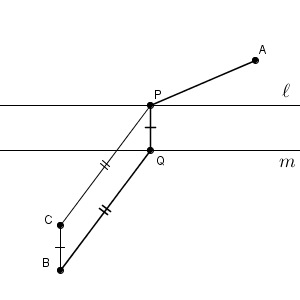
このことから、 $\mathrm{ AP+QB }$ は、 $\mathrm{ AP+PC }$ と同じなので、これが最小になるときを考えればいいことになります。こうなると簡単ですね。線分 $\mathrm{AC}$ と直線 $\ell$ との交点を $\mathrm{P}$ としたときが最小となります。
以上から、次のように作図できます。

こちらも、点に名前をつけて手順を書いてみます。
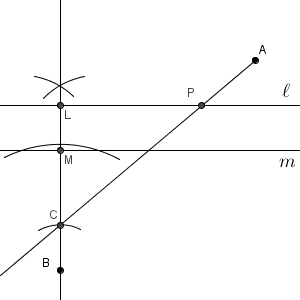
まず、点 $\mathrm{B}$ から直線 $m$ への垂線をひきます。この垂線と直線 $\ell,m$ との交点を $\mathrm{L, M}$ とします。 $\mathrm{B}$ が中心で半径が $\mathrm{LM}$ の円をかき、この円と垂線との交点を $\mathrm{C}$ とします($\mathrm{A}$ に近い方の点です)。
あとは、線分 $\mathrm{AC}$ と直線 $\ell$ との交点を作れば、これが点 $\mathrm{P}$ となります。これで完成です。
$\mathrm{ AP+BQ }$ は考えにくいですが、同じ長さである $\mathrm{ AP+CP }$ を使えば、いつ最小になるかがわかりやすくなります。
おわりに
ここでは、最短経路に関する問題を見てきました。2点間の距離が最小になるのは、2点を線分で結んだときになることを利用できるようにしましょう。