【応用】比例と反比例のグラフ
ここでは、1つのグラフに、比例のグラフと反比例のグラフが両方入っているような問題や反比例のグラフが2つ入っている問題を見ていきます。
比例と反比例のグラフ
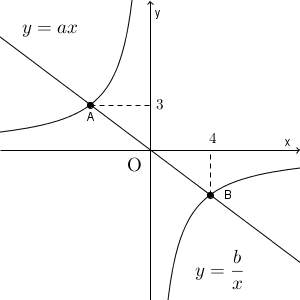
比例定数がわかっていませんが、これを求めるには、【標準】比例のグラフや【標準】反比例のグラフで見たように、通る点の座標がわかっていればいいですね。ただ、今の場合、点の座標の情報は完全にはわかっていません。
しかし、今までの比例や反比例のグラフを見てもわかる通り、これらのグラフは原点について対称です。このことから、今の場合、点A と点B は、原点について対称となります。
点Bの $x$ 座標が $4$ なら、点Aの $x$ 座標は、符号を入れ替えた $-4$ であることがわかります。また、点A の $y$ 座標は $3$ なので、点B の $y$ 座標は、 $-3$ であることがわかります。
点B の座標から、\[ -3=4a \]より、 $a=-\dfrac{3}{4}$ であること、\[ -3=\dfrac{4}{b} \]から、 $b=-12$ であることがわかります。
2つの反比例のグラフ
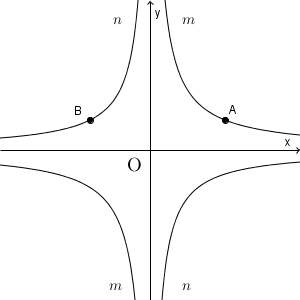
さらに、点C, 点D を、それぞれ、曲線 $m$, $n$ 上の点で、点A, 点B と $x$ 座標の絶対値が等しく、どちらも $y$ 座標がマイナスとなるようにとります。
この条件を満たすとき、四角形ABCD の面積は、点A の座標によらないことを、点A の座標を $(p, q)$ とおいて、説明しなさい。また、この面積を求めなさい。なお、座標の1目盛りを1cmとします。
「四角形ABCD の面積は、点A の座標によらない」というのは、点A がどんな座標でも、四角形ABCD の面積は変わらない、ということです。本当でしょうか。
いきなり面積を考え始めるのは難しいので、まずは点の座標を求めるところから考えていきましょう。点A の 座標を $(p, q)$ とおくように言われているので、この通りやってみます。ただ、この点は曲線 $m$ 上の点なので、\[ q=\dfrac{10}{p} \]が成り立ちます。
点B と点A の $y$ 座標は等しいので、 $q$ であることがわかります。 $x$ 座標は\[ q=-\dfrac{8}{x} \]を解いて、 $-\dfrac{8}{q}$ であることがわかります。
点C と点A の $x$ 座標の絶対値が等しく、点D と点B の $x$ 座標の絶対値が等しいのだから、点C, D は次のような点となります。
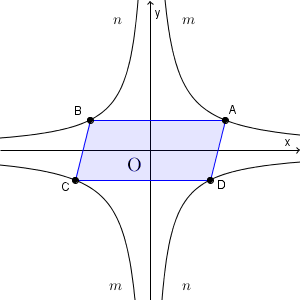
先ほどの例題のように、原点について対称移動した点だということがわかるので、点C の座標は $(-p,-q)$ であり、点D の座標は、 $\left(\dfrac{8}{q}, -q\right)$ であることがわかります。
さて、点A, B の $y$ 座標はともに $q$ で、点C, D の $y$ 座標はともに $-q$ であることから、AB と CD は平行であることがわかります。このことから、AB を底辺と考えると、これに高さを掛ければ、四角形ABCD の面積が求められることになります。
高さは、AB が $x$ 軸から $q$ だけ上にあり、CD が $x$ 軸から $q$ だけ下にあるので、高さは $2q$ cm であることがわかります。
一方、AB の長さは、A が $y$ 軸より $p$ だけ右にあり、B が $y$ 軸より $\dfrac{8}{q}$ だけ左にあるので、この2つを足したものが AB の長さになります。
ただ、 AB を表すのに $p,q$ 2つの文字があると厄介なので、一つ減らすことを考えましょう。 $p,q$ については、はじめに見たように、次の関係式が成り立つのでした。\[ q=\dfrac{10}{p} \]点A $(p,q)$ が $y=\dfrac{10}{x}$ のグラフ上にあるからですね。これを変形すれば、\[ p=\dfrac{10}{q} \]となります。これを利用すれば、面積をすべて $q$ を使って表すことができます。
以上から、四角形ABCD の面積は、\[ \left(\frac{10}{q}+\frac{8}{q}\right) \times 2q=36 \]となり、 $p,q$ が含まれない値が得られました。つまり、点A の座標によって、四角形ABCD の面積は変わらないことがわかり、面積は $36\mathrm{cm}^2$ であることがわかりました。
おわりに
ここでは、比例と反比例のグラフを両方含んだり、反比例のグラフが2つ含まれるような問題を見ました。今、どのグラフに注目しているのか、意識しながら考えるようにしましょう。