【応用】2つのおうぎ形
ここでは、2つの円や2つのおうぎ形を組み合わせた問題を見ていきます。
2つの円を組み合わせた問題
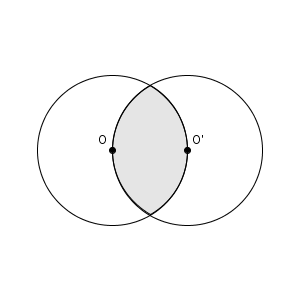
色のついた部分は変わった図形に見えますが、よく見ると、2つの弧で囲まれているだけですね。なので、弧の長さを求めればいいですね。半径がわかっているので、あとは中心角がわかれば求められます。
ただ、中心角はすこしわかりづらいです。中心角とは、今の場合、下の図の部分を指しています。
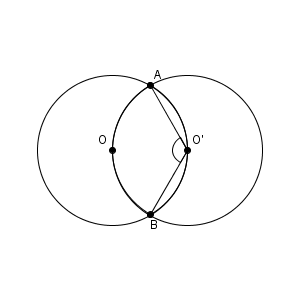
上の図では、弧$\mathrm{AOB}$ の中心角を表しています。 $\angle \mathrm{ AOB }$ や $\angle \mathrm{ AO'B }$ が中心角となります。
さて、今考えている図形では、「2つの円が互いの中心を通っている」状況ですが、これによって何がわかるでしょうか。中心角を求めるのに使えないか考えてみましょう。
弧の長さを求めるために角を求めたいのですが、実は線分に関する情報がたくさん含まれています。まず、 $\mathrm{ OA, OB, O'A, O'B }$ は、すべて半径なので $6\mathrm{ cm }$ です。しかも、 $\mathrm{ OO' }$ も半径なので、同じ長さです。
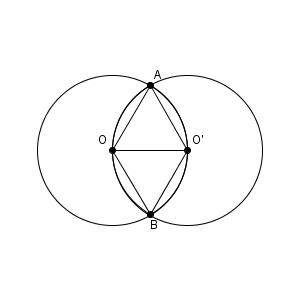
このことから、三角形 $\mathrm{ OAO' }$ と三角形 $\mathrm{ OBO' }$ はどちらも正三角形であることがわかります。こうして、中心角は両方とも $120^{\circ}$ だとわかるので、色のついた部分の周の長さは\[ 6\times 2\times \pi\times \frac{120}{360}\times 2=8\pi \]から、 $8\pi\mathrm{ cm }$ となることがわかります。
円や弧について考えているのに、正三角形を見つけないと角度がわかりません。半径はどこでも長さが同じですが、このことを利用すると、図の中に正三角形や正方形が見つかる場合があります。
2つのおうぎ形を組み合わせた問題
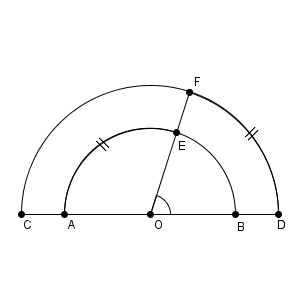
点$\mathrm{O}$ を通る直線と2つの半円との交点を $\mathrm{E, F}$ とすると、弧$\mathrm{AE}$ と弧$\mathrm{DF}$ の長さは同じになりました。このとき、$\angle \mathrm{ FOD }$ の長さを求めなさい。
「弧$\mathrm{AE}$ と弧$\mathrm{DF}$ の長さは同じ」とありますが、これがどのようなときなのかを考えないといけないですね。弧の長さを求めるには、半径と中心角が必要です。それぞれの半径はわかっていますが、中心角はどちらもわかりません。
ただ、2つの中心角の合計はわかります。 $\angle \mathrm{ FOD }$ と $\angle \mathrm{ EOA }$ は、合計すると半円の中心角となるので、 $180^{\circ}$ です。
これらを利用して、2つの弧の長さが同じであることを、方程式で表してみましょう。 $\angle \mathrm{ FOD }$ を $x^{\circ}$ とすると、弧 $\mathrm{DF}$ の長さは\[ 3\times 2\times \pi \times \frac{x}{360} \]となります。また、 $\angle \mathrm{ EOA }$ は、 $180^{\circ}-x^{\circ}$ なので、弧 $\mathrm{AE}$ の長さは\[ 2\times 2\times \pi \times \frac{180-x}{360} \]となります。この2つが等しいことを方程式で表して解くと
$$\begin{align*}
3\times 2\times \pi \times \frac{x}{360} &= 2\times 2\times \pi \times \frac{180-x}{360} \\[5pt]
3\times \frac{x}{360} &= 2\times \frac{180-x}{360} \\[5pt]
3x &= 2(180-x) \\[5pt]
3x+2x &= 360 \\[5pt]
x &= 72 \\[5pt]
\end{align*}$$と求められます。1行目から2行目では $2\pi$ で割っています。2行目から3行目では $360$ を掛けています。方程式を解くときに、いきなり掛け算を始めるのではなく、共通の部分を消してから計算するほうが楽になります。
こうして、 $\angle\mathrm{ FOD }=72^{\circ}$ と求められます。
図形の問題でも、このように方程式を利用して解く問題もあります。
おわりに
ここでは、2つの円や2つのおうぎ形が関連する問題を見てきました。半径の長さが等しいことを利用して正三角形を見つける問題や、方程式を利用して解く問題を見てきましたが、こういう方法は今後も使うことになります。