【標準】おうぎ形の弧の長さや面積
ここでは、おうぎ形の弧の長さや面積に関連する問題を見ていきます。
おうぎ形の弧の長さや面積を求める問題
おうぎ形の弧の長さと面積は、【基本】円とおうぎ形や【基本】おうぎ形などの面積の後半で見ています。円周の長さや円の面積に、360°に対する中心角の割合を掛ければいいのでしたね。
なので、この問題では、弧の長さは\[ 2\times 9 \times \pi \times\frac{150}{360}=\frac{15}{2}\pi \]より、 $\dfrac{15}{2}\pi\mathrm{ cm }$ と求められます。面積は\[ 9^2\times \pi \times \frac{150}{360}=\frac{135}{4}\pi \]より、 $\dfrac{135}{4}\pi \mathrm{ cm^2 }$ と求められます。
$\pi$ を使った計算に慣れていきましょう。
おうぎ形の中心角を求める問題
先ほどの例題では、半径と中心角から面積を求めましたが、今回は、半径と面積から中心角を求める、という流れです。
こうした問題では、中心角を $x^{\circ}$ とおいて方程式を作ってみましょう。こうすると、このおうぎ形の面積を $x$ を用いて表せば\[ 4^2\times\pi\times\frac{x}{360} \]となります。これが $12\pi$ になるので、次のようにして $x$ を求めることができます。
$$\begin{align*}
4^2\times\pi\times\frac{x}{360} &= 12\pi \\[5pt]
16\times\frac{x}{360} &= 12 \\[5pt]
x &= 12\times\frac{360}{16} \\[5pt]
&= 3\times 90 \\[5pt]
&= 270
\end{align*}$$となり、中心角は $270^{\circ}$ となることがわかります。
弧の長さは、この中心角を用いて、\[ 2\times 4 \times \pi \times \frac{270}{360}=6\pi \]だから、 $6\pi \mathrm{ cm }^2$ と求められます。
2つのおうぎ形
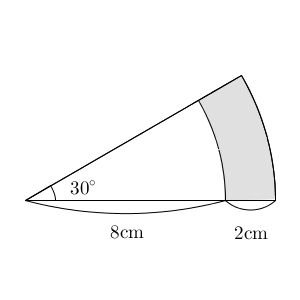
ピザの耳のような部分ですね。このような部分の面積を出す公式などは特にありません。今まで学んだ内容を応用して求めます。

この色のついた部分をよく見ると、大きなおうぎ形と小さなおうぎ形にはさまれた形になっています。そのため、大きなおうぎ形の面積から小さなおうぎ形の面積を引けば求められます。ピザの中央部分を食べると耳の部分が残る、というような求め方です。
小さなおうぎ形の半径は、 $8\mathrm{ cm }$ だとすぐにわかります。一方、大きなおうぎ形の半径は、小さなおうぎ形の半径より $2\mathrm{ cm }$ 長いのだから $10\mathrm{ cm }$ だとわかります。中心角は同じ $30^{\circ}$ ですね。
以上から、色のついた部分の面積は
$$\begin{align*}
&
10^2\pi\times \frac{30}{360}-8^2\pi\times \frac{30}{360} \\[5pt]
=&
100\pi\times \frac{1}{12}-64\pi\times \frac{1}{12} \\[5pt]
=&
\frac{100\pi-64\pi}{12} \\[5pt]
=&
3\pi
\end{align*}$$となり、 $3\pi\mathrm{ cm }^2$ だとわかります。
おわりに
ここでは、おうぎ形の弧の長さや面積に関連する問題を見てきました。最後の例題のように、公式をそのままの形では使えないような図形が出てくることもあります。公式が使えるように、わかりやすい形に分解するなどして求めるようにしましょう。