【標準】平行な線の作図
ここでは、平行な線の作図方法を見ていきます。この段階では教科書で取り上げられていないこともありますが、基本的な図形なので知っておいた方がいいでしょう。いくつかの方法を見ていきます。
平行な線の作図(垂線を利用)
次の図で、点 $\mathrm{P}$ を通り、直線 $\ell$ に平行な直線を作図する方法を考えてみましょう。
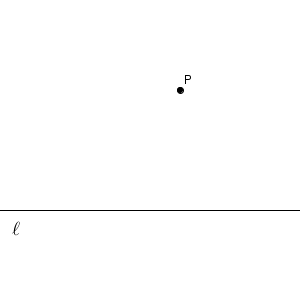
今まで、垂線や二等分線の作図方法を見てきましたが、平行な作図は出てきませんでした。しかし、これらを繰り返し使うことで、平行な直線を作図することができます。
平行な2直線は、【基本】点と直線との距離と作図で見たように、距離が一定だという性質があるのでした。
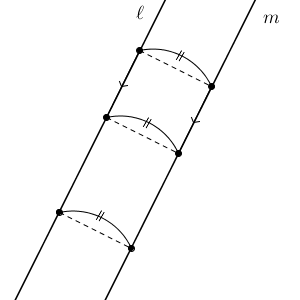
この図の見方を変えると、$\ell$ に平行な直線とは、 $\ell$ に垂直な直線 に垂直な直線、ということができます。少し複雑ですが、垂線の垂線を考えると、平行な直線が得られます。垂線の作図方法はわかっているので、これで平行な直線が作図できます。
先ほどの図に戻って作図をしてみましょう。まず、点 $\mathrm{P}$ を通り、直線 $\ell$ に垂直な直線を作図します(参考:【基本】垂線の作図(直線上にない点を通る)その2)。
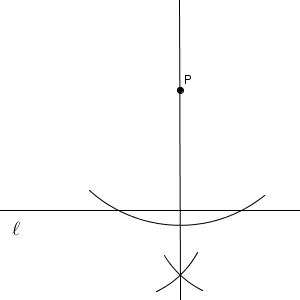
続いて、これに垂直で、点 $\mathrm{P}$ を通る直線を作図します(参考:【基本】垂線の作図(直線上の点を通る))。

こうして、垂線を2回かくことで、平行な直線を作図することができます。が、少し面倒ですね。以降では、もう少し楽な方法を見ていきます。
平行な線の作図(正方形を利用)
先ほど、垂線の垂線をかくことで、平行な直線を作図しました。しかし、2回垂線をかくのは少し面倒ですね。実は、1回目の垂線を作図したときに得られることを使えば、2回目の垂線の作図は不要になります。

上の図は1回目の垂線の作図が終わったところです。これにより、点 $\mathrm{P}$ と直線 $\ell$ との距離がわかります。垂線と $\ell$ との交点と点 $\mathrm{P}$ との距離ですね。平行な直線をかくには、直線 $\ell$ からこの距離だけ離れた点がもう1点わかればいいですね。
手っ取り早いのは、次のようにして正方形をかいてしまう方法です。こうすれば、直線 $\ell$ から同じ距離だけ離れた点を作図することができます。
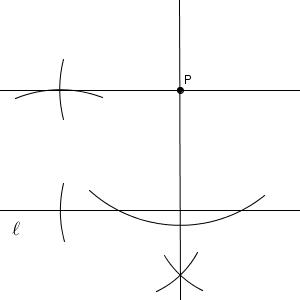
こうして、垂線をかいて、正方形を作ることで、平行な直線を作図することができます。ただ、実はもっと楽にできます。垂線をかくことすら不要です。
平行な線の作図(ひし形を利用)
先ほどは、平行な直線をかくために、点 $\mathrm{P}$ と直線 $\ell$ との距離を使って、正方形を利用しました。先ほどと少し図は違いますが、後半部分の作図は次のようになっていました。

上の図では、1辺の長さが点 $\mathrm{P}$ と直線 $\ell$ との距離の正方形を作っているのですが、平行な直線を作図するのに実は正方形が必要というわけではありません。ひし形でも十分です。

ひし形は同じ長さの線分を使えばできるため、コンパスと定規で作図できます。
このことから、次のような作図方法で平行な直線を作図することができます。まず、直線 $\ell$ 上の適当なところに点をとります。この点を点 $\mathrm{A}$ としましょう。点 $\mathrm{A}$ を中心とし、点 $\mathrm{P}$ を通る円をかきます。その円と直線 $\ell$ との交点を $\mathrm{Q}$ とします。

次に、点 $\mathrm{P, Q}$ を中心として、先ほどと同じ半径の円をかきます。交点を $\mathrm{R}$ とします。
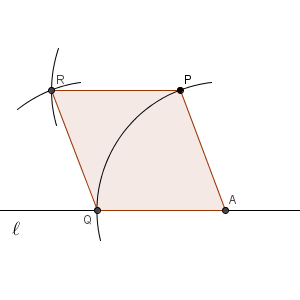
四角形 $\mathrm{APRQ}$ はすべての辺の長さが同じなのでひし形となり、 $\mathrm{AQ}$ と $\mathrm{PR}$ が平行になることがわかります。こうして平行な直線が作図できます。完成図は次のようになります。

はじめに適当なところに点をとる、というのは不思議な作図方法ですね。
おわりに
ここでは、平行な線を作図する方法を見てきました。垂線を2回かくというのが愚直なやり方ですが、最後の方法も楽なので覚えておきましょう。