【標準】垂線や二等分線の作図
ここでは、垂線や角の二等分線、垂直二等分線の作図を行う問題を見ていきます。
ある点に一番近い点
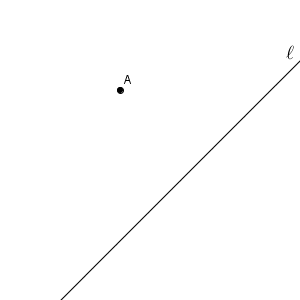
直接的に、「垂線や二等分線の作図」とは書かれていないので、まずは、どういう点をかけばいいのかを考えましょう。どのように作図するかは置いておいて、作図できたとしたらどうなるかを考えます。満たすべき条件もかき加えれば、次のようになります。

点 $\mathrm{A}$ を通る、直線 $\ell$ に垂直な線をひいて、直線 $\ell$ との交点を作図すればいいことがわかります。【基本】垂線の作図(直線上にない点を通る)その2 などを参考にして、次のように作図します。

「垂線」とは書いていませんが、「垂線」の作図が必要です。
2点から等距離にある点
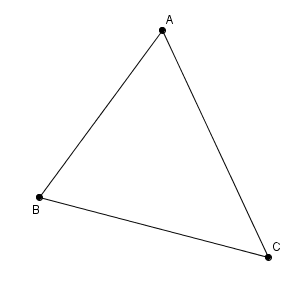
これも、完成図から考えます。満たすべき条件もかき加えれば、次のようになります。
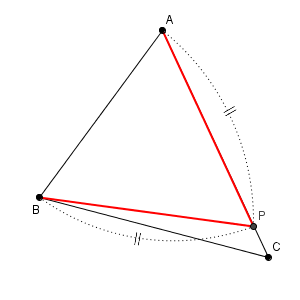
線分 $\mathrm{AP, BP}$ は同じ長さなので、点 $\mathrm{P}$ は辺 $\mathrm{AB}$ の垂直二等分線上にあることがわかります。垂直二等分線で折ると、 $\mathrm{AP, BP}$ がぴったりと重なるからです。
【基本】垂線二等分線の作図 の後半と同じような問題です。このリンク先で見たように、辺 $\mathrm{AB}$ の垂直二等分線をかき、辺 $\mathrm{AC}$ と交わった点が、点 $\mathrm{P}$ となります。

「2つの点からの距離が等しい点の集まり」を「垂直二等分線」に言い換えることが必要です。
2つの線分からの距離が等しい点
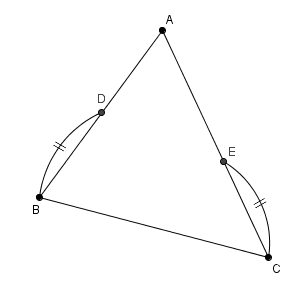
このとき、辺 $\mathrm{BC}$ 上に点 $\mathrm{P}$ をとると、三角形 $\mathrm{BDP}$, 三角形 $\mathrm{CEP}$ の面積が等しくなりました。点 $\mathrm{P}$ を作図しなさい。
三角形 $\mathrm{BDP}$, 三角形 $\mathrm{CEP}$ の面積が等しく、 $\mathrm{BD, CE}$ の長さが等しいので、これらを底辺として考えると、高さが等しくなることがわかります。つまり、点 $\mathrm{P}$ は次のようになっていることがわかります。
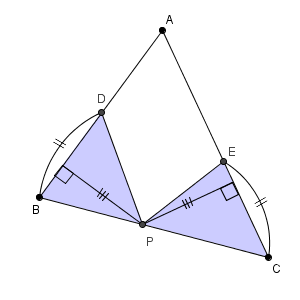
高さが等しいということは、辺 $\mathrm{AB, AC}$ からの距離が等しいということです。そのため、 $\mathrm{AP}$ で折り返すと、高さを表している線分はぴったりと重なります。このことから、点 $\mathrm{P}$ は、 $\angle \mathrm{ A }$ の二等分線上にあることがわかります。
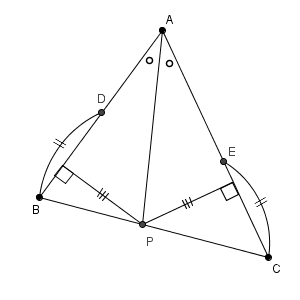
点 $\mathrm{P}$ を作図するには、 $\angle \mathrm{ A }$ の二等分線をかいて、辺 $\mathrm{BC}$ との交点を作ればいいことがわかります。【基本】角の二等分線の作図 で見た方法にしたがって作図します。
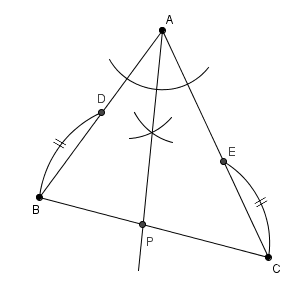
「面積と底辺が等しいから高さが等しい」→「2つの底辺からの距離が等しい」→「角の二等分線」と順番に言い換えていくことで、何を作図すればいいかを考えていきます。
この問題は、【基本】点と直線との距離と作図 とほとんどものを作図していますが、こちらのほうが、作図にいたるまでの考え方は難しいです。
おわりに
ここでは、垂線や二等分線の作図をする問題を見ました。「垂線や二等分線を作図しなさい」とは明記されていませんが、これらを作図することが答えとなるものを見てきました。何を作図すればいいのか、完成図から考えたり、言いかえを使ったりして考えていきましょう。