【標準】反比例のグラフと変域
ここでは、反比例のグラフを使って、変域を求める問題を見ていきましょう。
反比例のグラフと変域その1
変域とは、【基本】比例の性質で見たように、変数がとりうる値の範囲のことを言います。この問題であれば、 $x$ が2以上4以下の値をとるときに、 $y$ がどのような値をとるか、範囲を答えなさい、ということです。
比例のときにも似たような問題を解きました(参考:【標準】比例のグラフ)が、反比例は少し複雑なので、グラフを利用して考えてみましょう。
まずは、反比例 $y=\dfrac{12}{x}$ のグラフをかいてみましょう。変域のことは一旦忘れて、全体をかいてみます。
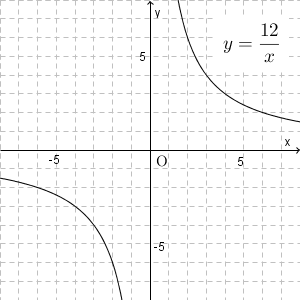
上のようになります。ここで、 $x$ の範囲を $2\leqq x \leqq 4$ としてみましょう。 $x$ 軸上で言えば、次の部分だけを考える、ということです。グラフの右上の部分だけが関係するので、右上の部分を拡大して考えてみます。

端を含むことを強調して示したい場合は、黒丸を使います。また、後で見るように、端を含まない場合は、白丸を使います。
次に、反比例 $y=\dfrac{12}{x}$ のグラフでは、どの部分に対応するかを考えます。 $x$ の対応する範囲とグラフの対応する範囲を考えると、次の部分になります。
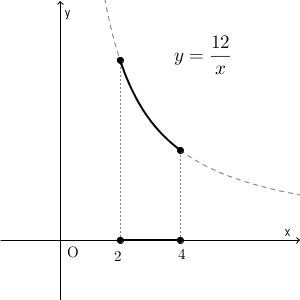
もとのグラフの太い実線の部分だけが対象で、残りの破線部分は対象外、ということです。
このことを利用して、 $y$ の値の範囲、つまり、上下にはどれだけ動くかを考えます。一番低いところは右下の部分、一番高いところは左上の部分なので、 $y$ の値の範囲は、次のようになります。
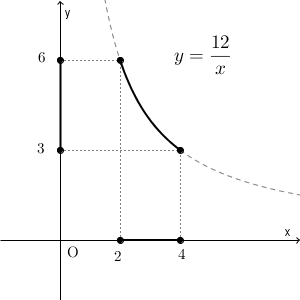
こうして、 $y$ の変域は、 $3\leqq y\leqq 6$ となることがわかります。グラフを見てもわかる通り、この範囲の値をすべてとることがわかります。
この問題であれば、 $y=\dfrac{12}{x}$ という式から、 $x$ が増えるほど $y$ が減ることがわかるので、グラフをかかなくても求められる、という人もいるかもしれません。ただ、以降の問題のように、マイナスが絡んでくると考えづらくなるので、グラフをかいて考える方がいいでしょう。
反比例のグラフと変域その2
今度は、 $x$ の変域にマイナスがついていますね。先ほどと同じように、全体のグラフを考え、 $x$ の変域に対応する部分をかく、という流れで考えていきます。
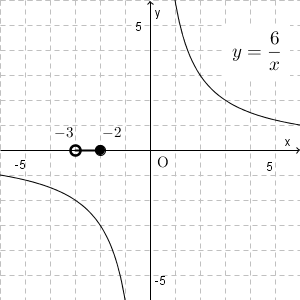
全体のグラフと、今考えようとしている $x$ の変域は上のようになります。 $x=-3$ の点は含みません。このように、端を含まないことを強調して示したい場合は、白丸を使います。
$x$ の変域を加味すると、 $y$ の変域は次のようになります。グラフの左下の部分だけが関係するので、左下の部分を拡大してみます。
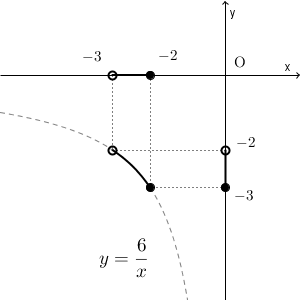
上の図から、 $y$ の変域、つまり、上下方向にとり得る値の範囲は、 $-3\leqq y\lt -2$ となることがわかります。 $y=-2$ は含まないので、 $-3\leqq y \leqq -2$ ではなく、 $-3\leqq y \lt -2$ となっている点に注意しましょう。
反比例のグラフと変域その3
今度は、反比例の式 $y=-\dfrac{4}{x}$ にマイナスがついています。これも流れは同じです。全体のグラフを考え、 $x$ の変域に対応する部分をかく、と考えていきます。
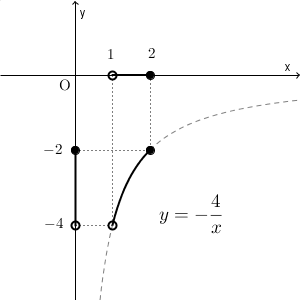
上の図から、 $y$ の変域、つまり、上下方向にとり得る値の範囲を見ると、 $-4\lt y\leqq -2$ となることがわかります。
おわりに
ここでは、反比例の式と $x$ の変域が与えられているときに、 $y$ の変域を求める方法を見てきました。グラフをかいて、対応する部分を見るようにすると、求めやすくなります。