【標準】一次方程式の利用(池の周り)
ここでは、一次方程式を利用して解く問題を見ていきます。速さに関する問題のうち、「池の周りを歩いたり走ったりする」系の問題を見ていきます。
池の周りを歩く問題
兄の歩く速さが分速80mだったとき、弟の歩く速さを求めなさい。
速さに関する問題は、【標準】一次方程式の利用(速さが変わる)などでも見ていますが、利用する関係は、
速さ × 時間 = 距離
です。今の問題で、何がわかっているかをおさえておきましょう。
歩き方は2通りあります。反対向きか同じ向きか、ですね。それぞれ歩いた時間はわかっています。兄の歩く速さもわかっているので、それぞれの場合で、兄の歩いた距離はわかります。
しかし、弟の歩く速さはわかりません。歩いた距離もわかりません。速さも距離もどちらもわからないのに、どうやって求めればいいのでしょうか。
ここで、池の周りを歩いて、二人が出会ったとき、追いついたときの動きを、図で見てみましょう。イメージをつかむためのものなので、問題文にある速さとは異なっている点に注意してください。
まず、反対向きに歩き出して、最終的に出会うまでのイメージは次のような動画になります。中央の円が池を表しているとします。
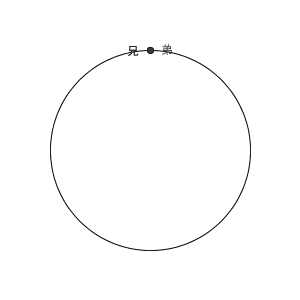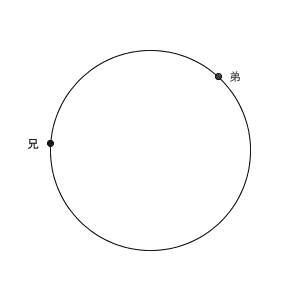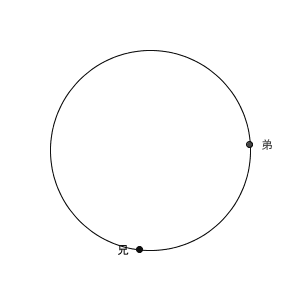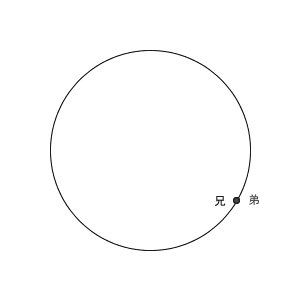
二人の距離が縮まって、最終的にはどこかで出会うわけですね。
一方、同じ向きに歩き出して、最終的に兄が弟に追いつくまでのイメージが次の動画です。追いつくまでに時間がかかるので、先ほどとスピードを変えています。

兄が弟に追いつくのだから、兄のほうがはやく歩くことになります。兄はたくさん歩いて、ようやく弟に追いつくことができます。
さて、それぞれの場合を詳しく見てみましょう。二人が反対向きに歩き出した場合は、次のような図になります。
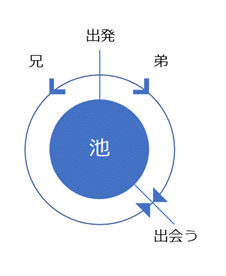
弟がどれだけの距離を歩いたかはわかりませんが、上の図から、兄と弟の歩いた距離を足すと、池の周りの長さに一致することがわかります。
では、兄が弟を追いかける場合だとどうなっているでしょうか。池の周りの長さに関連付けて、弟の歩いた距離を表せないでしょうか。
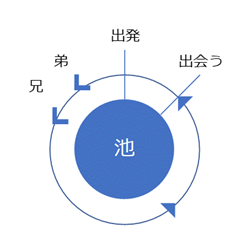
兄が弟に追いつくとき、二人の歩いた距離と池の周りの長さには、ある関係式が成り立ちます。上の図や、先ほどの動画をもう一度見直してみましょう。そうすれば、どういうときに「追いついた」と言えるかがわかると思います。
動画をよく見るとわかるかもしれませんが、兄が弟に追いつくとき、兄は弟の歩いた距離よりも、池1周分多く歩くことになります。
これらのことから、次の2つの関係式が成り立ちます。
<反対向きに歩くとき>
兄の歩いた距離 + 弟の歩いた距離 = 池の周りの長さ
<同じ向きに歩くとき>
兄の歩いた距離 - 弟の歩いた距離 = 池の周りの長さ
弟の歩いた距離はわかりませんが、歩く速さを、分速 $x$ mとすると、それぞれのケースで歩いた距離を $x$ を使って表すことができます。そうすれば、池の周りの長さを2通りで表すことで、方程式を作ることができます。
以上を踏まえると、次のような解答となります。
$$\begin{align*} 80\times 6+ 6x &= 80\times 42-42x \\[5pt] 6x+42x &= 80\times 42-80\times 6 \\[5pt] 48x &= 80\times (42-6) \\[5pt] x &= \frac{80\times 36}{48} \\[5pt] &= 60 \\[5pt] \end{align*}$$となる。よって、分速60mである。これは問題にあっている。
答:分速60m
教科書や参考書には、いきなり方程式が出てきて、なぜその方程式が成り立つのかわからないことがあるかもしれませんが、この問題では、池の周りの長さを2通りで表していることになります。
おわりに
ここでは、一次方程式を使う、池の周りを歩く問題を見てきました。
反対向きに歩いたときは、出会った時までに歩いた距離の和が、池の周り1周分になっていること、そして、同じ向きに歩いたときは、追いついたときまでに歩いた距離の差が、池の周り1周分になっていること、この2つを利用して、池の周りの長さを2通り表すことがポイントです。