【標準】対称移動に関する作図
ここでは、対象の軸や対称移動した後の図形を作図する問題を考えます。また、点対称移動についても合わせてみていきます。
対称移動に関する作図の問題
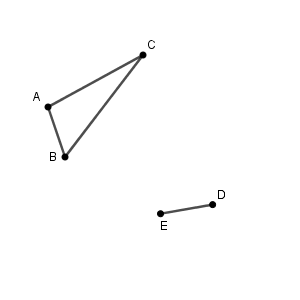
(1) 直線 $\ell$ を作図しなさい。
(2) 三角形 $\mathrm{ABC}$ を直線 $\ell$ について対称移動してできる三角形 $\mathrm{DEF}$ を作図しなさい。
まず、(1)の直線 $\ell$ を考えます。対称移動とは、そこで折り返すとぴったりと重なるように移動することでした(参考:【基本】対称移動)。どこで折り返せば、辺 $\mathrm{AB}$ と辺 $\mathrm{DE}$ が重なるでしょうか。
ぴったりと重なるときに、対応する点を結んで考えてみましょう。線分 $\mathrm{AD}$ は、直線 $\ell$ で折り返すとちょうど半分になって重なることから、直線 $\ell$ は線分 $\mathrm{AD}$ の中点を通り、線分 $\mathrm{AD}$ に垂直であることがわかります。
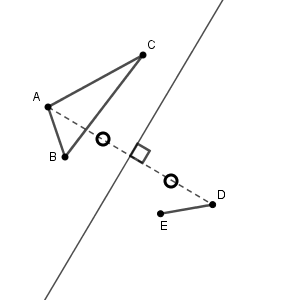
つまり、直線 $\ell$ は、線分 $\mathrm{AD}$ の垂直二等分線に一致します。そのため、直線 $\ell$ は次のように作図できます(参考:【基本】垂線二等分線の作図)。
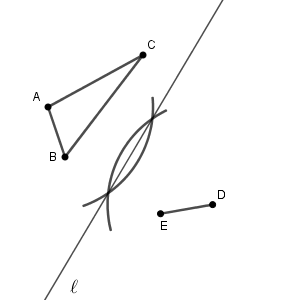
続いて、(2)を考えます。点 $\mathrm{F}$ が作図できればいいですね。先ほどとは逆に、線分 $\mathrm{CF}$ の垂直二等分線が直線 $\ell$ となるように、点 $\mathrm{F}$ を作図するにはどうするかを考えます。完成図から考えてみましょう。
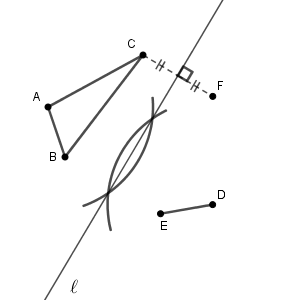
条件は2つあります。 $\mathrm{CF}$ と直線 $\ell$ が垂直に交わること、そして、 $\mathrm{C, F}$ から直線 $\ell$ からの距離が等しいことです。前者の作図はすでにやったことがある(参考:【基本】垂線の作図(直線上にない点を通る)その2)ので、まずは前者からやってみましょう。
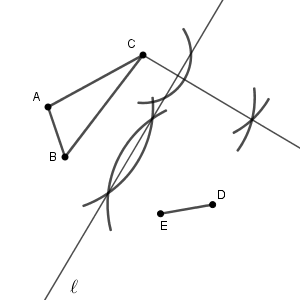
こうすると、 $\mathrm{C}$ から直線 $\ell$ までの距離もわかります。 $\ell$ と垂線の交点までの距離ですね。なので、この交点を中心として、 $\mathrm{C}$ までの距離だけ離れている点を、さきほどの垂線の上にとれば、それが $\mathrm{F}$ となります。
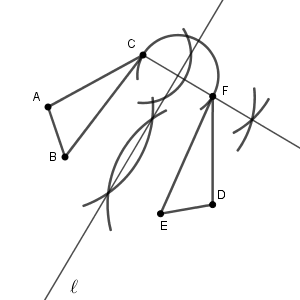
こうして $\mathrm{F}$ の場所がわかるので、三角形 $\mathrm{DEF}$ が作図できます。
この例題では、 $\mathrm{D, E}$ の2点がわかっていました。ただ、ここまでの作図方法を見てもわかる通り、 $\mathrm{E}$ の場所がわからなくても、直線 $\ell$ と三角形 $\mathrm{DEF}$ の作図はできます。 $\mathrm{E}$ の場所もわからない場合は、 $\mathrm{F}$ の作図でやったときと同じ方法で $\mathrm{E}$ も作図します。
点対称移動に関する作図の問題
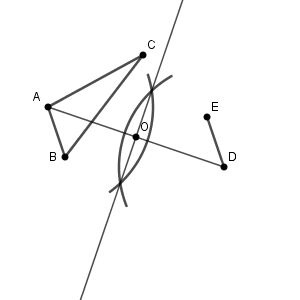
(1) 点 $\mathrm{O}$ を作図しなさい。
(2) 三角形 $\mathrm{ABC}$ を直線 $\ell$ について対称移動してできる三角形 $\mathrm{DEF}$ を作図しなさい。
点対称移動は、回転移動の特別版と考えられますが、対称移動の流れで作図方法を見ておきましょう。
(1)の点 $\mathrm{O}$ を考えます。点対称移動とは、ある点を中心として180度回転移動させることです。そのため、 $\mathrm{A, O, D}$ はこの順に一直線上にあり、 $\mathrm{ AO=DO }$ が成り立ちます。つまり、点 $\mathrm{O}$ は線分 $\mathrm{AD}$ の中点となります。
このことから、線分 $\mathrm{AD}$ の垂直二等分線と線分 $\mathrm{AD}$ との交点が点 $\mathrm{O}$ となります。
続いて、(2)を考えます。点 $\mathrm{F}$ が作図できればいいですね。先ほどとは逆に、線分 $\mathrm{CF}$ の中点が点 $\mathrm{O}$ となるように、点 $\mathrm{F}$ を作図するにはどうするかを考えます。完成図から考えてみましょう。
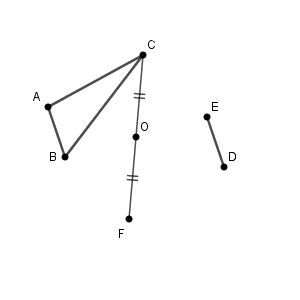
$\mathrm{C, O, F}$ は一直線上にあるので、 $\mathrm{F}$ は直線 $\mathrm{CO}$ 上にあります。さらに、 $\mathrm{ CO=FO }$ だから、 $\mathrm{O}$ を中心として、 $\mathrm{C}$ までの距離だけ離れている点を、直線 $\mathrm{CO}$ の上にとれば、それが $\mathrm{F}$ となります。

こうして $\mathrm{F}$ の場所がわかるので、三角形 $\mathrm{DEF}$ が作図できます。
この例題でも、 $\mathrm{D, E}$ の2点がわかっていましたが、 $\mathrm{E}$ の場所がわからなくても、直線 $\ell$ と三角形 $\mathrm{DEF}$ の作図はできます。 $\mathrm{E}$ の場所もわからない場合は、 $\mathrm{F}$ の作図でやったときと同じ方法で $\mathrm{E}$ も作図します。
おわりに
ここでは、対称移動、点対称移動に関する作図を見てきました。どのような移動かを考え、対称の軸や移動後の点がどのような条件を満たすかを考えてから、何を作図すればいいかを考えましょう。